Using gradient ascent to solve a discrete optimization spectral radius maximization problem.

Suppose that A is a random complex 40 by 40 matrix with independent Gaussian entries where the mean is zero and both the real and imaginary parts of each of the entries have variance 1 and are independent.

The goal is to find a matrix Z whose entries are all 0,1 and where the Hadamard product of Z with A has a maximized spectral radius.

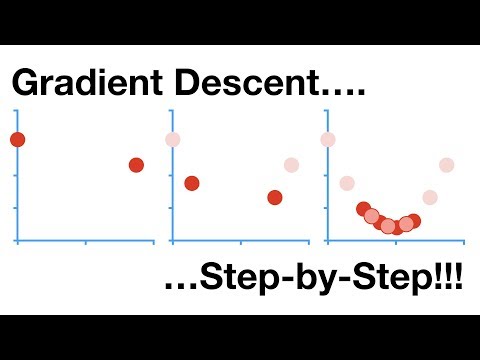
We can use discrete optimization techniques for solving this problem such as hill climbing or evolutionary computation, but for this problem we can also use gradient ascent.

To find the matrix Z, we set Z=sigmoid(X) where the sigmoid operation is performed elementwise and we use gradient ascent (we take the gradient of X) to maximize the spectral radius of the Hadamard product of Z with A. In the gradient ascent training, we increase the learning rate exponentially to make the training complete in a reasonable amount of time.

The notion of gradient ascent is not my own, but the use of gradient ascent to solve this particular problem is my own. While gradient ascent will not produce the solutions to this problem most efficiently, gradient ascent is reproducible in the sense that if we found the matrix Z multiple times using gradient ascent with only slight changes to the learning rates and optimizer, then we would obtain similar matrices both times.

This visualization shows how gradient ascent may be used to solve a discrete optimization problem.