filmov
tv
🔵23 - Method of Variation of Parameters 2 - Non-Homogeneous Differential Equations

Показать описание
In this lesson we shall learn how to solve the general solution of a 2nd order linear non-homgeneous differential equation using the method of variation of parameters.
Given a non-homogeneous differential equation: ay'' + by' + cy = G(x), where G(x) is not zero.
The general solution is given by: y = yc + yp.
To find the general solution, you first need to treat the given D.E as a homogeneous D.E, and solve its general solution - that becomes the general solution called the complementary function, yc.
For the yp, the particular integral, is obtained using the method of variation of parameter.
yp = u1y1 + u2y2.
With that we vary the parameters, by replacing c1 and c2 with two unknown functions of x.
To find u1 and u2, we first need to find the wronskian of the two functions.
00:00 - Introduction
04:15 - Ex 1
Playlists on various Course
1. Applied Electricity
2. Linear Algebra / Math 151
3. Basic Mechanics
4. Calculus with Analysis / Calculus 1 / Math 152
5. Differential Equations / Math 251
6. Electric Circuit Theory / Circuit Design
Make sure to watch till the end.
Like, share, and subscribe.
Thank you.
Given a non-homogeneous differential equation: ay'' + by' + cy = G(x), where G(x) is not zero.
The general solution is given by: y = yc + yp.
To find the general solution, you first need to treat the given D.E as a homogeneous D.E, and solve its general solution - that becomes the general solution called the complementary function, yc.
For the yp, the particular integral, is obtained using the method of variation of parameter.
yp = u1y1 + u2y2.
With that we vary the parameters, by replacing c1 and c2 with two unknown functions of x.
To find u1 and u2, we first need to find the wronskian of the two functions.
00:00 - Introduction
04:15 - Ex 1
Playlists on various Course
1. Applied Electricity
2. Linear Algebra / Math 151
3. Basic Mechanics
4. Calculus with Analysis / Calculus 1 / Math 152
5. Differential Equations / Math 251
6. Electric Circuit Theory / Circuit Design
Make sure to watch till the end.
Like, share, and subscribe.
Thank you.
🔵23 - Method of Variation of Parameters 2 - Non-Homogeneous Differential Equations
Differential Eqns. F22-23 -- Variation of parameters
mod06lec72 - Variation of Parameters
Method of variation of parameters#differentialequation #firstyearengineering #sem2 #semester_2 #csgt
23.Variation of parameter or wronskian method
Lec23/Higher Order ODEs/Method of Variation of Parameters
Variation of Parameters (nth order)
ODE- Variation of Parameters Method
unit 3 method of variation of parameter
7-2. Use the method of Variation of Parameters to find a particular solution to the 2nd order non-h…...
23. ODE || Chapter-13 || Method of Variation of Parameters || Honours 2nd year || NU
Differential Equations with Forcing: Method of Variation of Parameters
The Method of Variation of Parameters
Variation of parameters
Lecture 23(Variation of parameter method) Sept. 29
Variation of Parameters (Examples with 'a' not equal 1)
Variation of parameters - Solving Nonhomogeneous Second Order Differential Equations - Part 2
METHOD OF VARIATION OF PARAMETERS (ODE)
Variation of parameters | solving problems. #shorts
Methods of variation of parameters
Variation of parameters method - second order differential equations
Variation of Parameters | General Method of Solving Nonhomogeneous Differential Equations
🔵22 - Method of Variation of Parameters 1 - Non-Homogeneous Differential Equations
Variation of parameters - Solving Nonhomogeneous Second Order Differential Equations - Part 5
Комментарии
 0:21:20
0:21:20
 0:39:21
0:39:21
 0:28:13
0:28:13
 0:00:15
0:00:15
 0:06:41
0:06:41
 0:16:48
0:16:48
 0:08:16
0:08:16
 0:08:13
0:08:13
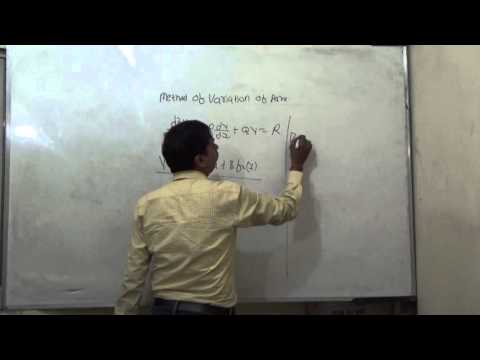 0:02:14
0:02:14
 0:00:33
0:00:33
 0:26:26
0:26:26
 0:23:25
0:23:25
 0:03:04
0:03:04
 0:09:50
0:09:50
 1:16:41
1:16:41
 0:20:42
0:20:42
 0:15:31
0:15:31
 0:14:59
0:14:59
 0:00:10
0:00:10
 0:00:21
0:00:21
 0:04:23
0:04:23
 0:11:46
0:11:46
 0:14:07
0:14:07
 0:12:31
0:12:31