filmov
tv
Why Are Slope and Area Opposite: The Fundamental Theorem of Calculus
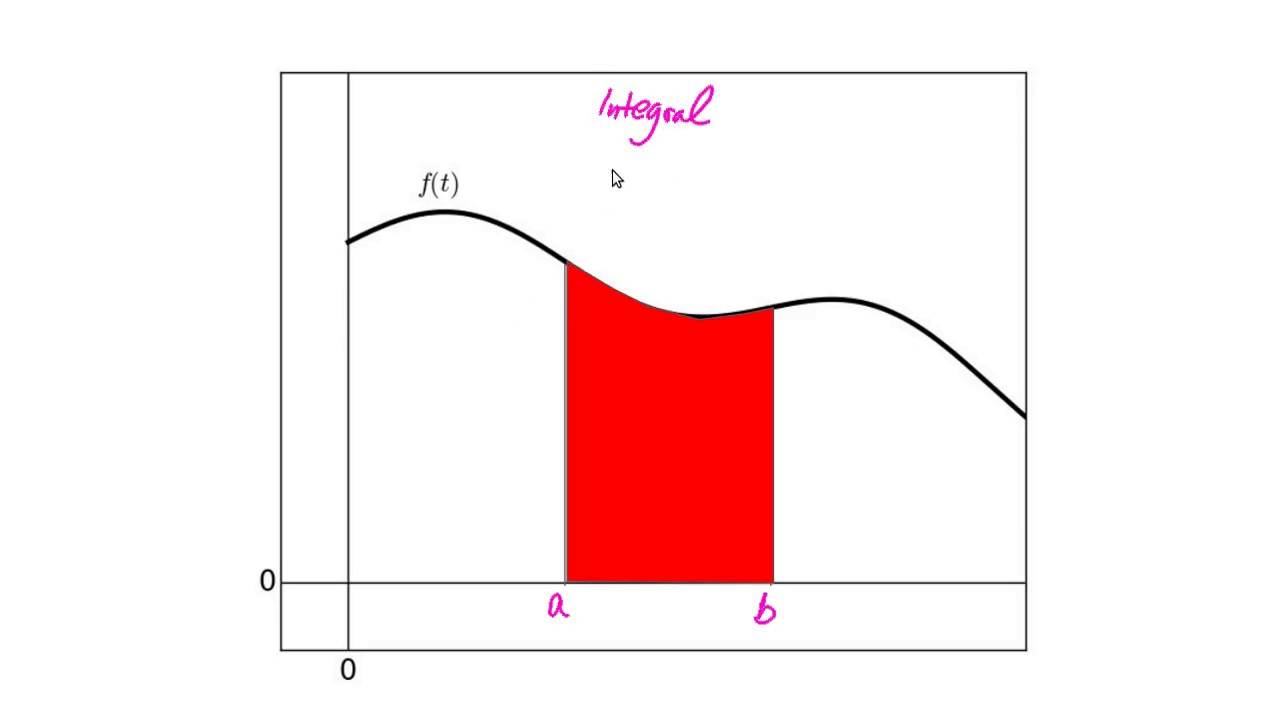
Показать описание
What does area have to do with slope? | Chapter 9, Essence of calculus
Why Are Slope and Area Opposite: The Fundamental Theorem of Calculus
The Slope Formula - Algebra
Calculus Based Physics Slope and Area
How is slope measured?
Calculus 5.4d - Some Comments on Slope and Area
Historic Context of the Continuous Slope Area Method
Derivative as slope and integral as area - AP Physics C
Finding The Slope Of A Property Using Google Earth
Slope Calculation
Find the slope of a graph
Slope | How To Find Slope || How To Find The Slope of a Line | Slope of a line #shorts #slope
Theory of the Slope-Area Method
Modern House Design Animation | slope land house design |
a modern building in land slide/steep slope area to.. #civilengineer #landslide #modernarchitechture
Physical Science 1.4f - Slope of a Position vs Time Graph
Use of slope and area in physics graphs
Problem Solving using a Motion Graph (Slope, Area, & Equations)
Slope and Grade
Calculating Slope Area from DEM in ArcGIS ||Slope area calculation || Arc Map 10.8
Multivariable calculus 1.2.2: Slope and area in polar coordinates
How To Build Houses On A Slope?
Steep Slope Houses – This is real ➽ Vivid example from Colombia
#civil engineering #important formulas #slope and deflection 🔥🔥
Комментарии
 0:12:39
0:12:39
 0:07:05
0:07:05
 0:08:47
0:08:47
 0:32:57
0:32:57
 0:01:31
0:01:31
 0:07:05
0:07:05
 0:15:14
0:15:14
 0:05:47
0:05:47
 0:01:04
0:01:04
 0:01:53
0:01:53
 0:02:41
0:02:41
 0:00:52
0:00:52
 0:04:34
0:04:34
 0:00:17
0:00:17
 0:00:11
0:00:11
 0:03:20
0:03:20
 0:06:45
0:06:45
 0:07:52
0:07:52
 0:09:50
0:09:50
 0:17:58
0:17:58
 0:07:26
0:07:26
 0:01:49
0:01:49
 0:00:26
0:00:26
 0:00:15
0:00:15