filmov
tv
Integrating 1/(1+cosx) in Two Ways

Показать описание
If you need to post a picture of your solution or idea:
#CalculusProblems #Integrals
EXPLORE 😎:
PLAYLISTS 🎵 :
#CalculusProblems #Integrals
EXPLORE 😎:
PLAYLISTS 🎵 :
Integrating 1/(1+cosx) in Two Ways
Integral of 1/(1 + cos x) dx
Integral of 1/cosx
Integral of 1/(1+cos(x) vs integral of sqrt(1+cos(x))
Indefinite Integral of 1/(1-cos(x))
Integration of 1/1-cosx (Solution)
How to integrate 1/cos(x)
Integral of 1 / (1- cosx)dx
weierstrass substitution, integral of 1/(1+sin(x)+cos(x))
How REAL Men Integrate Functions
Integral of 1/1-cosx
integral of 1/(2+cos(x)) , Weierstrass substitution
Integrate 1-cosx/1+cosx dx #maths #shorts #short #shortvideo #integration
How to integrate 1/cosx
Integral of 1/1+cosx #shortsfeed #shorts #viralshorts #education #integral #math #exercisequestion
Integral of 1/cos(x) = ln|tan(pi/4+x/2)|
integral battle#16, integral of 1/(1+cos(x)), integral of sqrt(1+cos(x))
Definite integral sqrt(1+cos(x)) trig identity and absolute value of cosine integral.
Solve the Integral problem 1/(1- Cosx) dx #mathsvideotech #integrals
Evaluate the integral : ∫ √(1+ cosx) dx
Integration By Trigonometric Functions, Exercise9.3 #6. ∫ dx/(1-cosx)
INTEGRAL‼️ of 1/cos x dx
Integral of sqrt(1-cosx) | HV math Academy
Integral of (1+sinx)/(1+cosx)
Комментарии
 0:09:03
0:09:03
 0:01:42
0:01:42
 0:05:50
0:05:50
 0:05:25
0:05:25
 0:03:18
0:03:18
 0:03:19
0:03:19
 0:03:21
0:03:21
 0:03:06
0:03:06
 0:02:34
0:02:34
 0:00:35
0:00:35
 0:02:55
0:02:55
 0:06:01
0:06:01
 0:00:55
0:00:55
 0:00:56
0:00:56
 0:00:46
0:00:46
 0:04:51
0:04:51
 0:08:31
0:08:31
 0:03:39
0:03:39
 0:00:57
0:00:57
 0:03:09
0:03:09
 0:02:57
0:02:57
 0:07:02
0:07:02
 0:02:40
0:02:40
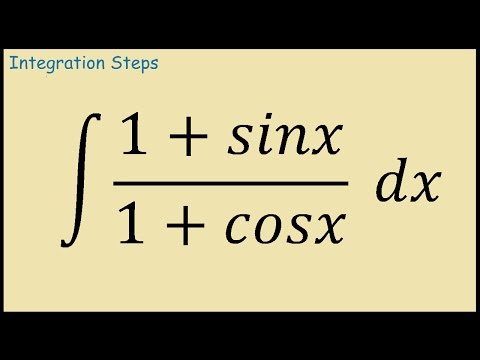 0:04:25
0:04:25