filmov
tv
Determinant of a 3x3 Matrix

Показать описание
In this video, I showed how to compute the determinant of a 3x3 matrix by first computing the cofactors or otherwise
How To Find The Determinant of a 3x3 Matrix
How To Find the Determinant of a 3x3 Matrix - The Easy Way!
Finding the determinant of a 3x3 matrix method 1 | Matrices | Precalculus | Khan Academy
Determinant of 3x3 Matrices, 2x2 Matrix, Precalculus Video Tutorial
Determinant of a 3x3 Matrix
Finding the determinant of a 3x3 matrix method 2 | Matrices | Precalculus | Khan Academy
Determinant of a 3x3 Matrix
Quickly Find the Determinant of a 3x3 Matrix
Ex 1: Determinant of 3x3 Matrix - Diagonal Method
Quick determinant trick
Determinant of a 3 by 3 Matrix
Find the Determinant of a 3x3 Matrix | Class 12
How to Find the Determinant of 3x3 Matrix?
❖ Finding the Determinant of a 3 x 3 matrix ❖
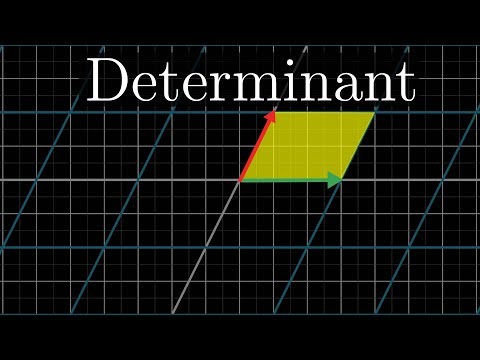
The determinant | Chapter 6, Essence of linear algebra
How to Find a 3x3 Determinant
How to find determinant of 3x3 Matrix Using calculator #viral #calculatortricks #youtubeshorts
Evaluating the Determinant of a Matrix
3 x 3 determinant | Matrix transformations | Linear Algebra | Khan Academy
Sarrus Rule | How To Fast Calculate The Determinant of A 3 x 3 Matrix | Linear Algebra
Determinant of 3x3 Matrix
How to find the Determinant of a 3x3 Matrix - Super Easy Method
How to find the Determinant of a 3x3 Matrix - Extremely Easy Shortcut
Determinant of a 3x3 Matrix Expansion of Minors
Комментарии
 0:11:31
0:11:31
 0:08:42
0:08:42
 0:02:39
0:02:39
 0:10:17
0:10:17
 0:12:15
0:12:15
 0:03:57
0:03:57
 0:09:34
0:09:34
 0:15:03
0:15:03
 0:03:34
0:03:34
 0:01:13
0:01:13
 0:07:10
0:07:10
 0:05:44
0:05:44
 0:05:29
0:05:29
 0:06:56
0:06:56
 0:10:03
0:10:03
 0:01:01
0:01:01
 0:01:00
0:01:00
 0:07:09
0:07:09
 0:10:01
0:10:01
 0:02:04
0:02:04
 0:13:40
0:13:40
 0:03:52
0:03:52
 0:06:39
0:06:39
 0:03:35
0:03:35