filmov
tv
Probability of a Touch in Finance using Python Monte Carlo Methods

Показать описание
We use Monte Carlo methods with Python to calculate the probability of a stock reaching a given price in a specified amount of time. The code simulates a large number of potential stock prices using the implied volatility to get the width of the normal distribution used to sample random numbers. The code then counts the number of runs where the target price is reached and estimates the probability by taking the ratio of that number with the total number of simulated runs.
Probability of Touching Options Trading Terminology & Trade Setup
How to Use Delta Probability of Touch
Probability of ITM vs. Probability of Touch
Probability of Profit Vs Touch With Options
How to Win More with Probability of Touch
Probability on Credit Spreads (Expiration vs. Prob. of Touch, 1% Rule)
What is Delta Probability of Touch
This Probability Rule Made Our Trades More Effective
What You Need to Know About Probability of Profit in 5 Minutes
Probability of a Touch in Finance using Python Monte Carlo Methods
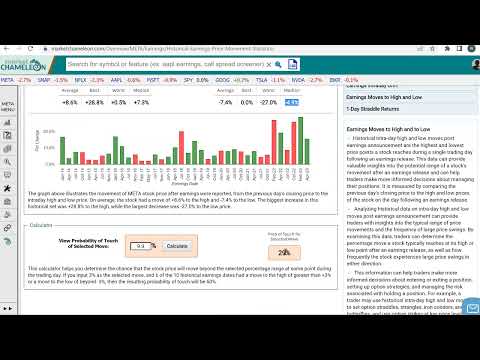
How to Calculate a Stock's Earnings Move Historical Probability of Touch
PROBABILITY OF ITM TOUCH
Probability of Touching vs. Probability of Expiring OTM: Very Different | Short Verticals
Option Chain Analysis: How To Estimate A Call Option's Probability of Touch
EP9 - Probability of Touch, managing a TSLA Iron Condor, and PATIENCE
How to Use Probability of Touching Column and Keep Your Cool When Stocks Wander | Short Verticals
How Expected Move and Probability of Touch Help the 0-DTE Strategy
Why Teaching Probability and Statistics is Crucial | Joe Rogan Experience ft. Neil Degrasse Tyson
Why You’re WRONG about Probability of Profit?
Calculate the Probability of Price reaching any level
What is the Probability of Reaching 50% of Max Profit?
Supply and demand zone not working? How to trade using supply and demand zones explained.
TRADING PROBABILITIES | PROBABILITY OF PROFIT EXPLAINED | Option Trading | Option Sailor
Probability with a touch of geometry -- MrMathTalk
Комментарии
 0:09:59
0:09:59
 0:08:03
0:08:03
 0:07:06
0:07:06
 0:10:37
0:10:37
 0:22:54
0:22:54
 0:24:01
0:24:01
 0:07:33
0:07:33
 0:08:10
0:08:10
 0:05:00
0:05:00
 0:18:25
0:18:25
 0:05:27
0:05:27
 0:03:44
0:03:44
 0:45:12
0:45:12
 0:07:10
0:07:10
 0:07:43
0:07:43
 0:44:25
0:44:25
 0:29:34
0:29:34
 0:00:54
0:00:54
 0:06:38
0:06:38
 0:10:02
0:10:02
 0:11:15
0:11:15
 0:00:38
0:00:38
 0:17:11
0:17:11
 0:02:41
0:02:41