Laurent Series for sin(1/z)

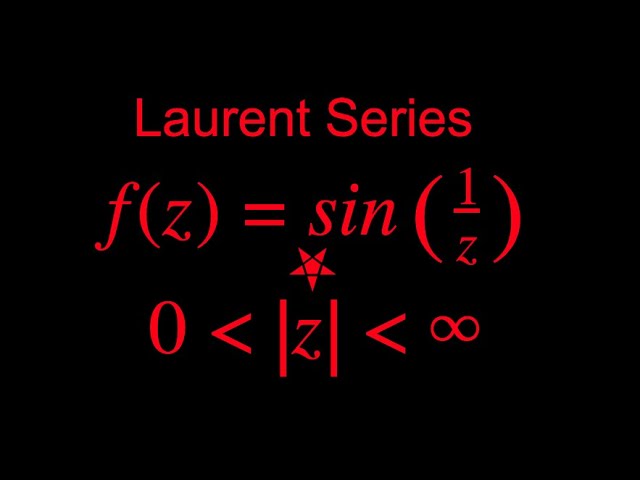
preview_player
Показать описание
Episode #000054
Monday, January 25th, 2021

One of the simplest examples of a Laurent Series, we will today expand sin(1/z) in the area of the complex plane for absolute values of z greater then zero but less than infinity.
Example taken from page 234 of "Basic Complex Analysis" (3rd Edition) by Jerrold E. Marsden and Michael J. Hoffman.
  1. pentagramprime
  2. pentagramprime
  3. sin(1/z)
  4. Laurent Series
  5. Complex Analysis
Рекомендации по теме
Laurent Series for 0:03:22

Laurent Series for sin(1/z)

Laurent Series Explained 0:13:56

Laurent Series Explained | How to Determine Laurent Series | Complex Analysis #9

[Complex Analysis] Find 0:01:31

[Complex Analysis] Find the Laurent Series for sin(2z)/z^3 when |z| is greater than 0

Laurent Series for 0:05:14

Laurent Series for e^z over z+1

Find the Residue 0:09:16

Find the Residue and Type of Singularity for sin(1\z)

Example of Laurent's 0:14:04

Example of Laurent's Series | L16 | TYBSc Maths | Complex Power Series @ranjankhatu

[Complex Analysis] Find 0:03:10

[Complex Analysis] Find the Laurent Series for z/(z+1)(z-2) when |z| is greater than 2

Laurent Series and 0:06:41

Laurent Series and Trigonometry

what is the 0:03:37

what is the residue of sin(z)÷z⁶ using laurent series

Laurent Expansion (Series) 0:07:21

Laurent Expansion (Series) || Example 1|| Complex Analysis MAT324

Laurent Reihen 2 0:06:34

Laurent Reihen 2 ►Laurent Reihe von sin(1/z)

Laurent Series for 0:02:17

Laurent Series for e^z/z^2

Find the Residue 0:10:02

Find the Residue and Type of Singularity for e^1/z

Taylor's and Laurent's 0:28:20

Taylor's and Laurent's Series Examples (complex analysis)

Example of Laurent's 0:23:47

Example of Laurent's Series | L 14 | TYBSc Maths | Complex Power Series @ranjankhatu

problem on taylor's 0:16:10

problem on taylor's series in complex analysis|problem on laurent series|Theta Classes

problems on laurent 0:18:49

problems on laurent series|complex integration in complex analysis|Theta Classes

What is the 0:12:55

What is the Laurent Series for cosec(z)

Laurent Series for 0:05:20

Laurent Series for f(z) = 1/(z + z^2) for |z| greater than 1

19. Taylor's and 0:11:25

19. Taylor's and Laurent's Series | Problem#1 | Most Important | Complete Concept

Laurent Series - 0:05:56

Laurent Series - A First Example

Taylor Series of 0:06:47

Taylor Series of sinz | L3 | TYBSc Maths | Complex Power Series @ranjankhatu

Find the Laurent 0:14:01

Find the Laurent Series and use the Ratio Test to find the Annulus of Convergence

Residue Theorem Function 0:09:14

Residue Theorem Function with Laurents Series

Комментарии
Автор

amazingly well explained video. I always talk myself like this while i am solving math questions lol

kefal
Автор

simple, straightforward, thanks a lot, you saved me

alejandroviciedo
Автор

Love the humor, thanks for the explanation :)

juancanekortegasanchez
Автор

Thansk for the simple explanation:). I was wondering if i could apply this same technique of replacing trig-functions with their taylor expansion for this problem: (cos(z^2)-1)/z^3 at z=0

DkGriefer
Автор

Can you tell me if the domain for the series expansion is 0<|z|<∞

Then the expansion of sin(1/z) is valid in the region |1/z|<∞. So how do we arrive at the solution and prove the domain 0<|z|<∞ is valid ?

gokuvegeta