filmov
tv
Algebra - Ch. 32: Application of Linear Equations (8 of 11) Linear Demand Equation: Example 1

Показать описание
To donate:
We will solve: If the price of tomatoes is $4/pound. The demand is 1 pound per customer per week. For each decrease of $1 per pound the demand increases by 1 pound. Find the equation and graph.
Next video in this series can be seen at:
Algebra - Ch. 32: Applications of Linear Equations (1 of 11) Types of Applications
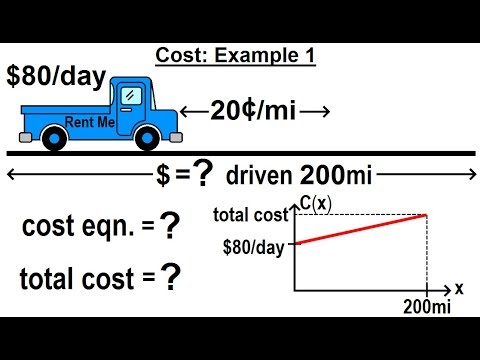
Algebra - Ch. 32: Application of Linear Equations (4 of 11) Cost: Example 1
Algebra - Ch. 32: Applications of Linear Equations (2 of 11) Depreciation: Example 1
Algebra - Ch. 32: Application of Linear Equations (11 of 11) Supply and Demand Equilibrium Point
Algebra - Ch. 32: Application of Linear Equations (8 of 11) Linear Demand Equation: Example 1
Algebra - Ch. 32: Application of Linear Equations (7 of 11) Profit: The Break Even Point
Algebra - Ch. 32: Application of Linear Equations (9 of 11) Linear Demand Equation: Example 2
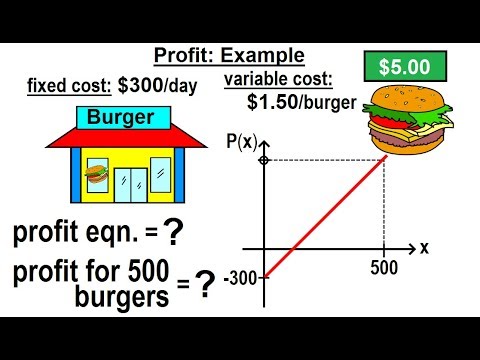
Algebra - Ch. 32: Application of Linear Equations (6 of 11) Profit: Example
write down the cube of /chapter 8 / questions 21 to 32 / algebra
Algebra - Ch. 32: Application of Linear Equations (5 of 11) Cost: Example 2
Algebra - Ch. 32: Application of Linear Equations (10 of 11) Linear Supply Equation
Algebra - Ch. 32: Applications of Linear Equations (3 of 11) Depreciation: Example 2
How to Answer Any Question on a Test
Basic Algebra Tips
Memorization Trick for Graphing Functions Part 1 | Algebra Math Hack #shorts #math #school
Algebra - Ch. 0.6: Basic Concepts (32 of 36) Algebraic Expressions in Combination: Set 1
How To Solve Absolute Value Equations, Basic Introduction, Algebra
Amazing Algebra Workbook With Solutions
Algebra - Ch. 30: Linear Equations (32 of 33) Find A Line Perpendicularto a Given Line
Algebra 32 - Solving Mixture Problems with Linear Equations
How to Solve First Degree Equations , Intermediate Algebra , Lesson 32
Algebra for Beginners | Basics of Algebra
Algebra - Ch. 5: Polynomials (5 of 32) How to Add Polynomials
ALGEBRA & PRE-ALGEBRA REVIEW: Ch 1 (32 of 53) Solving Algebraic Equations: Solve x=?
Комментарии
 0:06:30
0:06:30
 0:04:42
0:04:42
 0:05:59
0:05:59
 0:04:33
0:04:33
 0:05:29
0:05:29
 0:03:01
0:03:01
 0:07:00
0:07:00
 0:05:59
0:05:59
 0:04:30
0:04:30
 0:04:05
0:04:05
 0:04:06
0:04:06
 0:04:23
0:04:23
 0:00:27
0:00:27
 0:00:48
0:00:48
 0:00:15
0:00:15
 0:05:21
0:05:21
 0:04:21
0:04:21
 0:08:47
0:08:47
 0:04:05
0:04:05
 0:10:46
0:10:46
 0:05:02
0:05:02
 0:37:09
0:37:09
 0:02:08
0:02:08
 0:02:43
0:02:43