filmov
tv
An integral for 1/n!
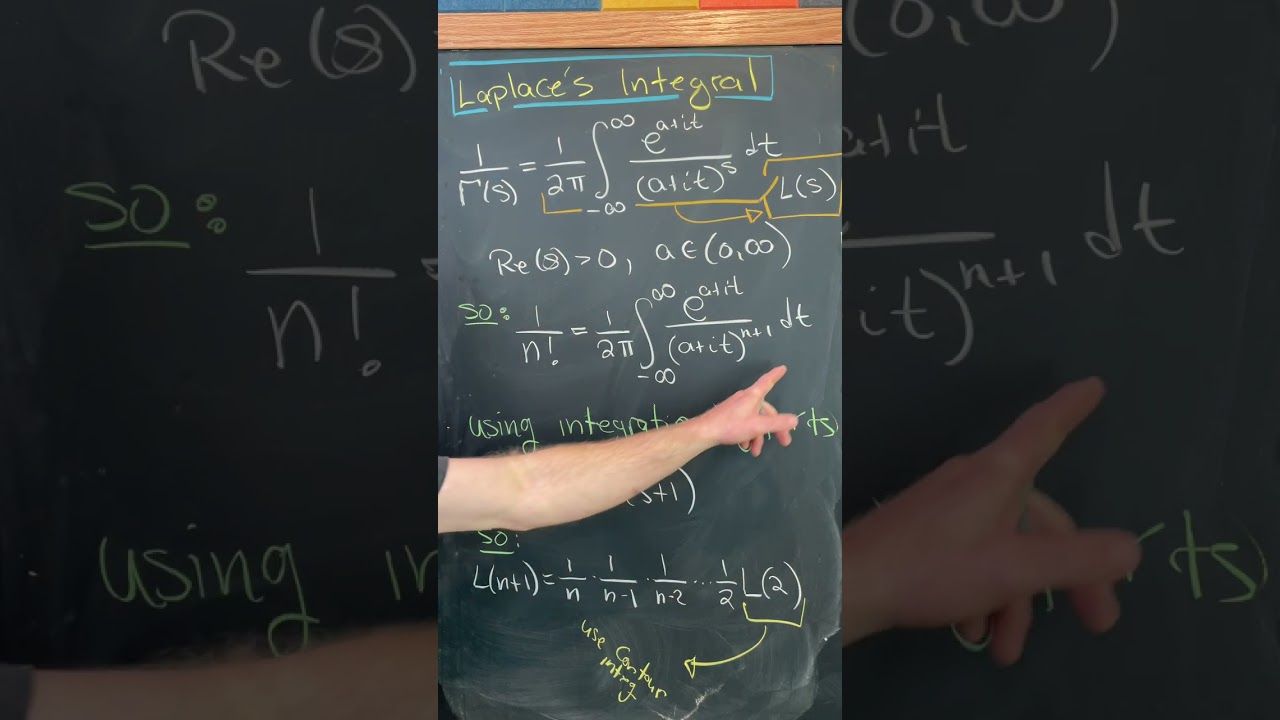
Показать описание
🌟Support the channel🌟
🌟my other channels🌟
🌟My Links🌟
🌟How I make Thumbnails🌟
🌟Suggest a problem🌟
🌟my other channels🌟
🌟My Links🌟
🌟How I make Thumbnails🌟
🌟Suggest a problem🌟
integral test, series of 1/(n*sqrt(ln(n))), calculus 2 tutorial
An integral in about 7 minutes
How REAL Men Integrate Functions
Evaluate integral by interpreting it in terms of areas
Complex Analysis: Integral of 1/(x^n+1) feat. pizza contour
The Integral of 1/x EXPLAINED. It's NOT what you think...
How to use the integral test for infinite series
a spectacular solution to the Basel problem (sum of 1/n^2 via a complex integral)
Integral 1/x^n + 1 from 0 to infinity
Determine if series converges or diverges. {1/(n ln n)}. The Integral Test. [2, infinity)
Integral 1/x^n + 1 from 0 to infinity
How to Find a Definite Integral using Riemann Sums and the Limit Definition: Quadratic Example
Complex Analysis: Integral of ln(x)/(x^n+1) using Contour Integration
A great integral calculus review in one problem!!
An integral in less than 5 minutes
Integral of lnx
Find the Limit of SUM((1/n^3)(i - 1)^2) as n approaches infinity
Introduction to integral calculus | Accumulation and Riemann sums | AP Calculus AB | Khan Academy
If I did this in 1734 I'd be World Famous
Fundamental Theorem of Calculus Part 1
Determine if series converges or diverges. {n e^n}. Integral Test for Series [1, infinity)
Use integral test to determine is series converges or diverges. { (1/n^5) }
Find the values of p for which the series converges. {1/(n(ln n)^p)}. Integral Test
Series of n(1+n^2)^p, sect11.3#31
Комментарии
 0:07:03
0:07:03
 0:07:18
0:07:18
 0:00:35
0:00:35
 0:04:51
0:04:51
 0:36:33
0:36:33
 0:03:12
0:03:12
 0:09:47
0:09:47
 0:22:27
0:22:27
 0:23:31
0:23:31
 0:04:31
0:04:31
 0:10:39
0:10:39
 0:13:18
0:13:18
 0:29:50
0:29:50
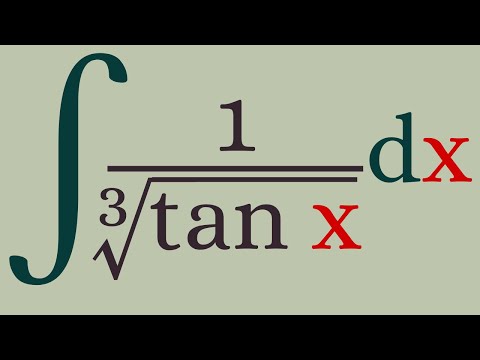 0:19:26
0:19:26
 0:04:32
0:04:32
 0:01:26
0:01:26
 0:06:29
0:06:29
 0:04:52
0:04:52
 0:03:57
0:03:57
 0:11:30
0:11:30
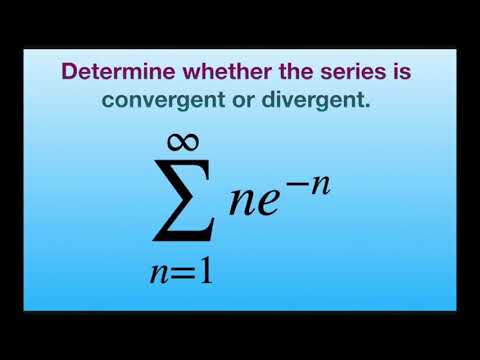 0:06:03
0:06:03
 0:02:23
0:02:23
 0:09:09
0:09:09
 0:05:41
0:05:41