filmov
tv
Fourier Transform Example
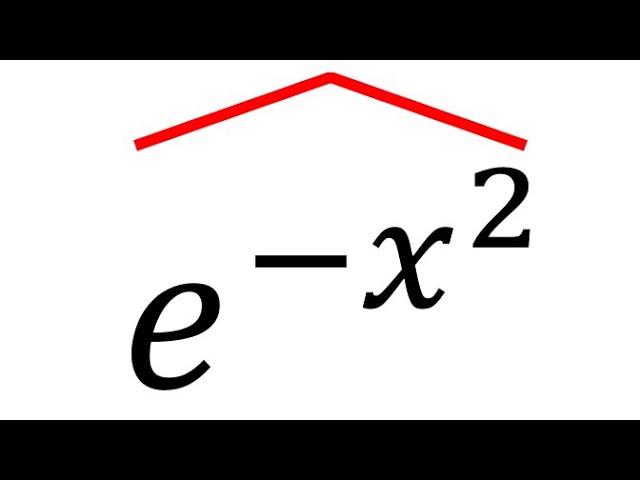
Показать описание
Fourier Transform Example
Fourier transforms are hard!! Which is why it would be nice to have a concrete example of a Fourier transform, which we do precisely in this video. Here we calculate the Fourier transform of the Gaussian function e^-x^2 or exp(-x squared) and the beautiful result is that it is again a Gaussian! This self-similarity or fractal property will be crucial when we'll solve the heat equation using the Fourier transform
Fourier transforms are hard!! Which is why it would be nice to have a concrete example of a Fourier transform, which we do precisely in this video. Here we calculate the Fourier transform of the Gaussian function e^-x^2 or exp(-x squared) and the beautiful result is that it is again a Gaussian! This self-similarity or fractal property will be crucial when we'll solve the heat equation using the Fourier transform
Fourier Transform Equation Explained ('Best explanation of the Fourier Transform on all of YouT...
Fourier Analysis: Fourier Transform Exam Question Example
Electrical Engineering: Ch 19: Fourier Transform (10 of 45) Find Fourier Transformation: Ex. 1
But what is the Fourier Transform? A visual introduction.
How to Compute a FOURIER SERIES // Formulas & Full Example
Fourier Transform properties : examples
Fourier Transforms! Example problem part 1
Fourier Transform (Solved Problem 1)
Introduction to the Fourier Transform (Part 1)
Why do we use the Fourier Transform?
Fourier Transform Examples
Fourier Transform Example Problem
How to compute a Fourier series: an example
An Introduction to the Fourier Transform
The Fourier Series and Fourier Transform Demystified
Fourier series
CT Fourier Transform || Examples 4.2, 4.3, 4.4 & 4.5 || S&S 4.1(2)
Fourier Transform Example Rectangular Pulse
Discrete Fourier Transform - Example
Fourier Transform Maths Explained #fouriertransform #maths #mathematics
Fourier Transform Examples and Solutions | Problem #28 | Numericals or Problems on Fourier Transform
Fourier Transform Examples and Solutions | Inverse Fourier Transform
Examples of Fourier Series
Computing the Fourier Series of EVEN or ODD Functions **full example**
Комментарии
 0:06:26
0:06:26
 0:08:02
0:08:02
 0:07:05
0:07:05
 0:20:57
0:20:57
 0:13:16
0:13:16
 0:05:44
0:05:44
 0:08:34
0:08:34
 0:10:09
0:10:09
 0:13:03
0:13:03
 0:00:59
0:00:59
 0:09:03
0:09:03
 0:04:14
0:04:14
 0:08:25
0:08:25
 0:03:20
0:03:20
 0:14:48
0:14:48
 0:01:00
0:01:00
 0:19:54
0:19:54
 0:11:06
0:11:06
 0:06:02
0:06:02
 0:00:59
0:00:59
 0:07:10
0:07:10
 0:27:33
0:27:33
 0:13:56
0:13:56
 0:09:34
0:09:34