filmov
tv
Integral of tan(x)*sec^3(x), tan sec approach, calculus 2 tutorial

Показать описание
Integral of tan(x)*sec^3(x), tan sec approach
----------------------------------------
#blackpenredpen #math #calculus #apcalculus
----------------------------------------
#blackpenredpen #math #calculus #apcalculus
Integral of tan(x)*sec^3(x), tan sec approach, calculus 2 tutorial
sec^3 x tan x dx, Evaluate the indefinite integral.
Integration of tan^3 x sec^3 x
Evaluate the Integral tan x sec^3 x dx U-Substitution.
Trigonometric Integrals Powers of Secant and Tangent sec^3(x)*tan^3(x)
Integral of tan^3(x)*sec(x), calculus 2 tutorial
integral tan(3x) sec(3x) dx , secante por tangente
Integral of tan^3x*sec^4x (read pinned comment)
Evaluate the Integral sec^3 x tan x dx with substitution rule
Integral of sec^3(x)tan(x) - Integral example
Integral of tan^3x, with tan and sec
Techniques of Integration - Trigonometric Integrals: 06. tan^3(x)sec^3(x)
Evaluate the Integral tan^5 x sec^3 x dx U-Substitution. Example 24. Trigonometric
Integration by u Substitution: Integral of tan^3(x)sec^3(x) dx
171. Integral de tangente quinta por secante cúbica. TRIGONOMETRICA. EJERCICIO RESUELTO.
155. Integrales trigonométricas con secante y tangente explicadas por CASOS.
Evaluate the Integral tan^3 x sec x dx U-Substitution. Example 25. Trigonometric
integral of tan^2(x)*sec(x), calculus 2 tutorial
my favorite calculus 2 trigonometry integral (two results off by a constant)
Integral dari tan^(5)x sec^(3)x dx adalah… | Integral Trigonometry Explanation eps.1 | how to solve...
Integral of tan(x)sec^2(x) dx (ILIEKMATHPHYSICS)
Integral of tan^m(x) sec^n(x)
Integrating Powers of tan(x) and sec(x) with an Even Power of sec(x)
integration of tanx/secx+tanx | integration of tanx/(secx+tanx) | integration of tanx | class 12...
Комментарии
 0:02:14
0:02:14
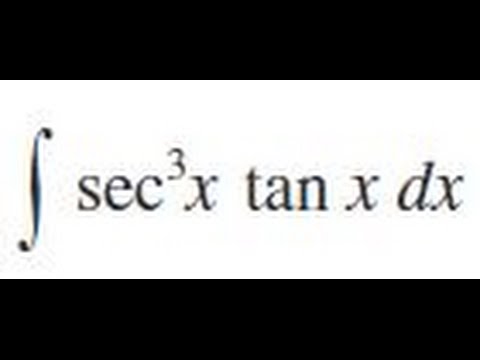 0:00:51
0:00:51
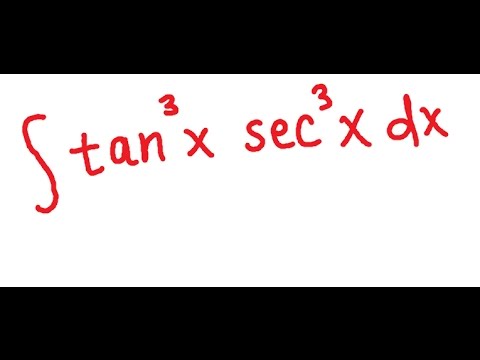 0:02:58
0:02:58
 0:02:05
0:02:05
 0:03:19
0:03:19
 0:02:40
0:02:40
 0:01:14
0:01:14
 0:04:17
0:04:17
 0:02:40
0:02:40
 0:02:30
0:02:30
 0:02:46
0:02:46
 0:04:05
0:04:05
 0:04:25
0:04:25
 0:02:01
0:02:01
 0:07:50
0:07:50
 0:10:24
0:10:24
 0:02:21
0:02:21
 0:04:10
0:04:10
 0:07:05
0:07:05
 0:11:59
0:11:59
 0:01:20
0:01:20
 0:09:08
0:09:08
 0:03:27
0:03:27
 0:03:47
0:03:47