filmov
tv
What is a Theorem, Corollary, Conjecture, Lemma, Axiom, and Proposition?

Показать описание
In this video, I will explain the differences between a theorem, corollary, conjecture, lemma, axiom, and proposition. You need to know these terminologies if you are taking a class about proofs or discrete mathematics. A proposition is a statement that is either true or false. An axiom is a statement that we assume to be true (self-evidently true) and we do not need to prove it. A lemma is a small result that has been proved, and it is used to prove a theorem. A theorem is a significant result that has been proved. A corollary is a theorem that follows on from another theorem. A conjecture is something that someone (usually a famous person) says is true but they have not been able to prove or disprove it.
What is a Theorem, Corollary, Conjecture, Lemma, Axiom, and Proposition?
What is a Theorem, a Corollary, an Axiom, a Lemma
Corollary 1 of Euler's Theorem Formula and Proof
Inscribed Angle Theorem Corollary | Maths
Theorem, Lemma, Corollary, Axiom and Conjecture. Are they Same? | Discrete Mathematics
Mean Value Theorem: Corollary Theorems
What is the difference between a Theorem, a Lemma, and a Corollary? with examples.
Axiom, Theorem, Lemma, Corollary
Corollary of Thales theorem( Basic Proportionality Theorem)
What is the corollary of the exterior angle theorem ?
🔵 Theory Theorem Hypothesis Postulate Corollary Axiom - Theory Postulate Corollary Axiom Meaning
Euler's Theorem |Corollary 1
AXIOMS -POSTULATES -THEOREM- COROLLARY - Basics
5.3.1 Theorem, Proof, & Corollary
Proof of Fundamental theorem corollary in Graph theory.
what is corollary? Understanding Corollaries: Key Points and Significance in Mathematics
Corollary of Basic Proportionality Theorem | Class 10 | Geometry | Math's |2020
Difference between Axioms, Definition, Lemma, Theorem, Corollary, Conjecture, Equation, and Formula
Terminologies; Proof,Axiom(or postulate),Theorem,Hypothesis,premise,Lemma,Corollary,Conjecture
Theorem and Corollary Lecture-5 EUCLID GEOMETRY (class-9)
Inscribed Angle Theorem: Corollary Properties
UNIVERSAL TRUTHS:- AXIOMS & POSTULATES. STATEMENT, THEOREM & COROLLARY - All Definitions| CL...
Theorem + corollary
Mathematics: What's the difference between theorem, lemma and corollary? (8 Solutions!!)
Комментарии
 0:03:00
0:03:00
 0:01:38
0:01:38
 0:07:23
0:07:23
 0:02:15
0:02:15
 0:04:38
0:04:38
 0:06:56
0:06:56
 0:01:00
0:01:00
 0:08:47
0:08:47
 0:12:00
0:12:00
 0:03:38
0:03:38
 0:15:51
0:15:51
 0:06:32
0:06:32
 0:05:30
0:05:30
 0:10:38
0:10:38
 0:04:29
0:04:29
 0:00:39
0:00:39
 0:07:11
0:07:11
 0:09:45
0:09:45
 0:01:30
0:01:30
 0:05:41
0:05:41
 0:06:34
0:06:34
 0:11:57
0:11:57
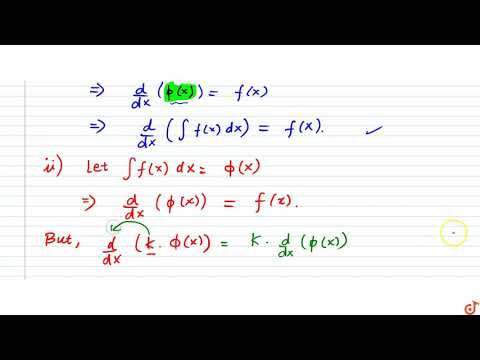 0:08:52
0:08:52
 0:04:11
0:04:11