filmov
tv
Given the endpoints of the minor axis and vertices find the equation of the ellipse

Показать описание
Learn how to write the equation of an ellipse from its properties. The equation of an ellipse comprises of three major properties of the ellipse: the major radius (a), the minor radius (b) and the center (h, k). The ellipse is vertical if the major radius in vertical and the ellipse is horizontal if the major radius is horizontal.
The center of an ellipse is halfway between the major/minor axis. When given the vertices of an ellipse, the major radius of an ellipse is the distance between the center of the ellipse and its vertices. When given the co-vertices of an ellipse, the minor radius of an ellipse is the distance between the center of the ellipse and its co-vertices.
After obtaining the center, the major and the minor radius, they are plugged into the equation of an ellipse to obtain the desired equation.
Timestamps:
0:00 Intro
1:30 Start of Problem
Corrections:
7:17 I miswrote the equation, it was supposed to be (y-2)^2
Follow us on
#conicsections #ellipseconicsections
The center of an ellipse is halfway between the major/minor axis. When given the vertices of an ellipse, the major radius of an ellipse is the distance between the center of the ellipse and its vertices. When given the co-vertices of an ellipse, the minor radius of an ellipse is the distance between the center of the ellipse and its co-vertices.
After obtaining the center, the major and the minor radius, they are plugged into the equation of an ellipse to obtain the desired equation.
Timestamps:
0:00 Intro
1:30 Start of Problem
Corrections:
7:17 I miswrote the equation, it was supposed to be (y-2)^2
Follow us on
#conicsections #ellipseconicsections
Find the Equation of a Circle Given Endpoints of Diameter
Can You Find the Equation of a Circle Given Only the Endpoints of the Diameter?
Given the endpoints of the diameter of a circle, find its equation.
Finding Endpoint Given Midpoint
Find the endpoint when given midpoint and other endpoint ex 1
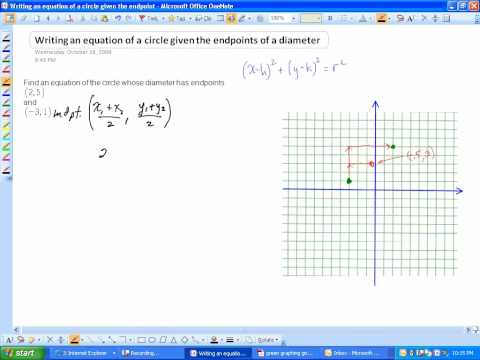
Writing an equation of a circle given the endpoints of the diameter
Conics given the endpoints of a circle find the equation
Find the center of a circle given the endpoints of a diameter
How to fix CORS Errors EASILY in your .NET 9 API!
Ex 1: Find Standard Equation of a Circle Given the Endpoints of a Diameter
Finding the Equation of a Circle Given the Endpoints of a Diameter
Conic Sections (Circle): Given only two endpoints of the diameter.
Find the Equation of the Circle Given the Endpoints of the Diameter
Finding the Equation of an Ellipse Given the Endpoints of the Major Axis and c
Equation of a circle given the endpoints of the diameter.
How to Write Equation of the Circle Given the Endpoints of the Diameter
Finding the Center-Radius Form of a Circle Given the Endpoints of the Diameter
Write the equation of a circle given the endpoints of the diameter
Equation of a circle given the endpoints of the diameter
Writing an equation of a circle given the endpoints of a diameter.wmv
Writing an equation of a circle given the endpoints of a diameter
Find Standard Form of Equation of Circle Given Endpoints of a Diameter
Endpoints of Diameter - Circle
[Tagalog Tutorial] - How to Find the Endpoints of the Latus Rectum | Conic Sections - Parabola
Комментарии
 0:02:01
0:02:01
 0:08:53
0:08:53
 0:02:49
0:02:49
 0:02:04
0:02:04
 0:04:33
0:04:33
 0:13:37
0:13:37
 0:06:54
0:06:54
 0:03:40
0:03:40
 0:08:35
0:08:35
 0:04:30
0:04:30
 0:03:55
0:03:55
 0:09:51
0:09:51
 0:04:36
0:04:36
 0:01:59
0:01:59
 0:05:18
0:05:18
 0:10:14
0:10:14
 0:03:21
0:03:21
 0:08:25
0:08:25
 0:06:46
0:06:46
 0:07:34
0:07:34
 0:03:35
0:03:35
 0:06:54
0:06:54
 0:03:18
0:03:18
![[Tagalog Tutorial] -](https://i.ytimg.com/vi/lZES5Hn2YW8/hqdefault.jpg) 0:06:54
0:06:54