filmov
tv
Solving the Bernoulli Differential Equation x^2(dy/dx) + y^2 = xy

Показать описание
How to solve a Bernoulli Differential Equation
The Bernoulli Equation // Substitutions in Differential Equations
Bernoulli's Equation For Differential Equations
How to solve Bernoulli differential equations
How to Solve Bernoulli Differential Equations (Differential Equations 23)
🔵16 - Bernoulli Differential Equations (dy/dx + p(x)y = q(x)y^n)
Solve a Bernoulli Differential Equation (Part 1)
Bernoulli First Order Equations - Example 1
Bernoulli Differential Equations: Solution Methods and Exercises
Bernoulli differential equation example #1
Bernoulli Differential Equations
solving a hard Bernoulli differential equation
Solve a Bernoulli Differential Equation (Part 2)
Bernoulli Differential Equation (with a missing solution)
Solving a Bernoulli Differential Equation
Ex: Solve a Bernoulli Differential Equation Using an Integrating Factor
❖ Bernoulli Equation for Differential Equations , Part 1 ❖
Bernoulli's Differential Equation | How to solve Bernoulli Differential Equation in urdu-ODE
How to Solve a Bernoulli Differential Equation
Bernoulli's Equation
Bernoulli Differential Equation dy/dx = y(xy^2 - 1)
Bernoulli's Differential Equation | Reducible to linear Differential Equation | Problem 1 | Mat...
Solving a Bernoulli Differential Equation (Example)
Bernoulli Differential Equations (MM-9.6-18)
BERNOULLI EQUATION || How to reduce it into the linear differential equation ?? || Mathematics ||
Комментарии
 0:09:19
0:09:19
 0:20:03
0:20:03
 0:05:30
0:05:30
 1:43:35
1:43:35
 0:28:21
0:28:21
 0:08:43
0:08:43
 0:04:50
0:04:50
 0:11:16
0:11:16
 0:09:05
0:09:05
 0:09:27
0:09:27
 0:13:13
0:13:13
 0:09:12
0:09:12
 0:09:26
0:09:26
 0:17:15
0:17:15
 0:09:13
0:09:13
 0:10:26
0:10:26
 0:13:20
0:13:20
 0:11:29
0:11:29
 0:08:22
0:08:22
 0:14:22
0:14:22
 0:10:35
0:10:35
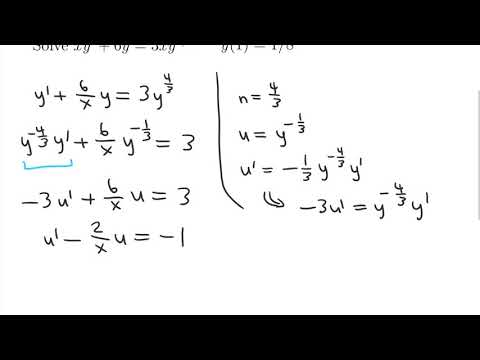 0:06:19
0:06:19
 0:01:38
0:01:38
 0:07:26
0:07:26