A Fundamental Theorem of Calculus for Series!!

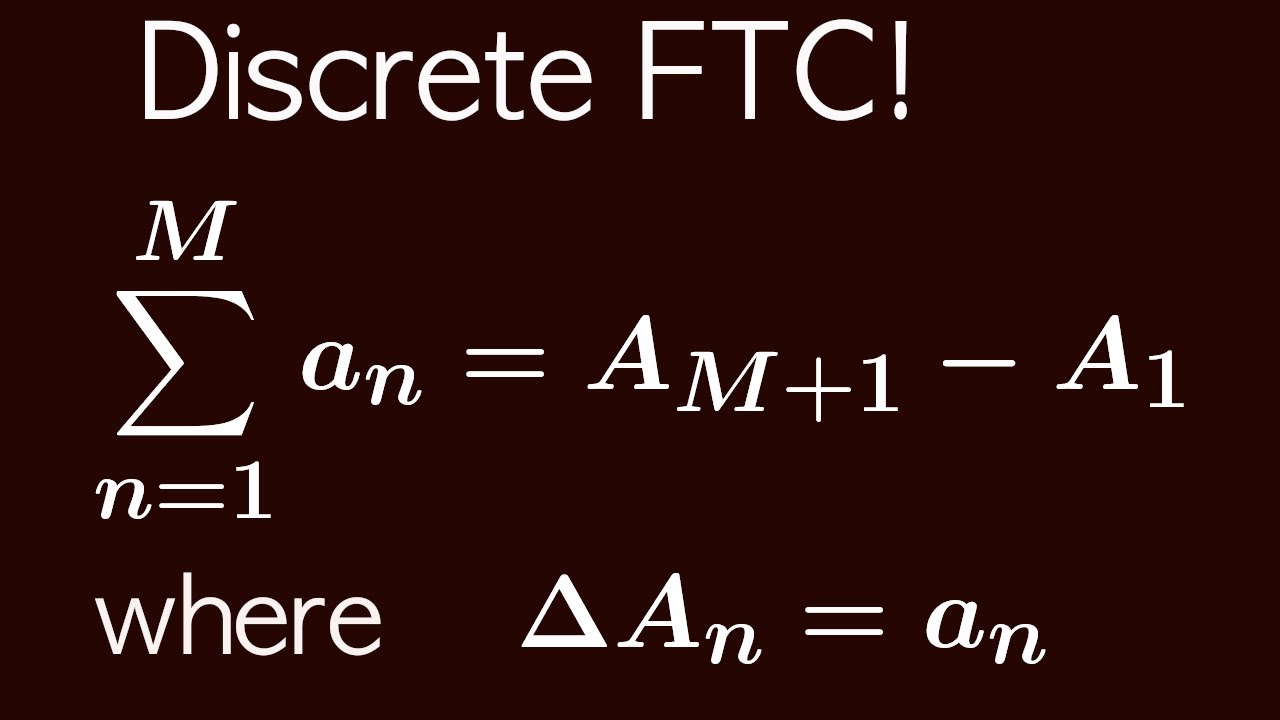
Показать описание

We present the discrete derivative, the discrete anti-derivative, and the Fundamental Theorem of Discrete Calculus. This leads us to a technique of finding sums of finite series using methods that look like those for definite integrals.

If you liked this trick, tell your Calculus professor and let's try an make it more widely popular.

Рекомендации по теме

Комментарии

I'm surprised this channel isn't that known, it's very good content for math lovers and the explanations are very good and understandable.

איתןגרינזייד

Summation by parts (which is the discreet analogue of integration by parts) is an effective technique very close to your FTC and worth considering.

gregoryrubalsky

At 6:00 I don't think that's correct as (-2/3)^n = -2^n * 3^-n != -2 * 3^-n-1 = -2/3 * (1/3)^n

ketzunet

The discrete derivative of (1/3)^n can be rewritten as -2/3^(n+1).

krisbrandenberger

This is so cool! I really like this! Make more videos covering this topic please!!

DragonKidPlaysMC

If you let M approach infinity, couldn't you find closed-form expressions for certain infinite sums? It looks like it works for the geometric series

ByteOfCake

This is giving me signals and systems flashbacks.

timtheenchanter

Why is it better to define the discrete derivative as the "forward" difference [ f(n+1) - f(n) ] as opposed to the "trailing" difference [f(n) - f(n-1)] ? Or for that matter the difference where f(n) is in the center? i.e. [ f(n+1) - f(n-1) ] /2 - divide by 2 since delta(n) is now = 2.
All we are doing here is finding the slopes of the secants where delta(n) = 1. I'm thinking that [ f(n-1) - f(n+1) ] /2 - the average slope where f(n) is square in the middle might be a better choice.
So for f(n) = n^2: [ (n+1)^2 - (n-1)^2 ] /2 = 2n.
I hope someone sees this as this video is 3 years old.
My reason for asking is that I have found a remarkable property of the harmonic sequence involving the "rate of decrease" - in a discrete kind of way - at h(n), but unsure which difference gives a better interpretation. I'm leaning toward [ f(n-1) - f(n+1) ] /2. Any ideas?

ianfowler

I saw Sigma symbol for so called discrete antiderivative
(by the way Leibniz intoduced integral symbol as the first letter of word Summa)

holyshit

This is the intuition I have for the usual FTC

smiley_

Really love your spastic summation signs! 😎Σ😎Σ😎Σ

perappelgren

This method gives sigma ( from n = 1 to M) [ n^2 ] = M ( M + 1 ) ( 2M - 5 ) / 6

but the answer from calculus class is M ( M + 1 ) ( 2M + 1 ) / 6

michaelempeigne

8:42 you forgot +C!!!! Yes that also applies to discrete

helloitsme

A Fundamental Theorem of Calculus for Series!!

Fundamental Theorem of Calculus Part 1

Integration and the fundamental theorem of calculus | Chapter 8, Essence of calculus

The Fundamental Theorem of Calculus: Redefining Integration

Fundamental theorem of calculus (Part 1) | AP Calculus AB | Khan Academy

Fundamental Theorem of Calculus 1 | Geometric Idea + Chain Rule Example

The fundamental theorem of calculus (fast AI lesson)

Fundamental Theorem of Calculus Explained | Outlier.org

Calculus 1 Lecture 4.5: The Fundamental Theorem of Calculus

Finding the exact area: The Definite Integral | Mathematical Methods | MaffsGuru.com

Fundamental Theorem of Calculus Parts 1&2

Fundamental Theorem of Calculus - Part I

Proof of fundamental theorem of calculus | AP Calculus AB | Khan Academy

What is the Fundamental Theorem of Calculus?

What does area have to do with slope? | Chapter 9, Essence of calculus

Calculus Class 11 Fundamental Theorem Interview

Fundamental theorem of calculus (Part 2) | AP Calculus AB | Khan Academy

Real Analysis | The Fundamental Theorem of Calculus

Fundamental Theorem of Calculus Part 2

3 Levels of Proving the Fundamental Theorem of Calculus | #SoME3

02 - Fundamental Theorem of Calculus, Part 1 - Learn Antiderivatives & Derivatives

1st Fundamental Theorem of Calculus PROOF | Calculus 1 | jensenmath.ca

1st Fundamental Theorem of Calculus | AP Calculus | Calculus 1 #shorts

The Fundamental Theorem of Calculus - Full Tutorial

Calculus AB/BC – 6.4 The Fundamental Theorem of Calculus and Accumulation Functions