filmov
tv
Golden limit

Показать описание
Limit using Monotone Sequence Theorem
I am back from summer vacation! In this video, I calculate an interesting limit using the monotone sequence theorem. It might have to do with bunnies, who knows? :)
I am back from summer vacation! In this video, I calculate an interesting limit using the monotone sequence theorem. It might have to do with bunnies, who knows? :)
Golden limit
How to Solve the Golden Limit Challenge
DARKSIDE- 'Golden Limit (Live at Spiral House)' (Official Audio)
23. Challenge: A golden limit
Golden Proof - Numberphile
Exercise 1: Limit of a Sequence and the Golden Ratio (Minus 1)
Golden Limit
Golden Limit
You have reached your request limit for the hour
HARD TRAP Beat Instrumental *Golden* (Prod. By Limit Beats)
🔴Sbi Credit Card 😱Limit Rs.221000
The Hacker Simon Cowell Gets The Golden Buzzer Full Performance Britain's Got Talent 2025 Audit...
LIMIT BREAK + CELESTIAL GOLDEN GUN DAMAGE
New Golden Super Saiyan Four!? Super Saiyan 4 Limit BREAKER! #shorts #dragonball
Amex Gold Card Credit Limit
Sky's the Limit | Persona 4: the Animation (OP 1) | PT-BR/ENG
How to Get UNLIMITED Money In No Limit Drag Racing 2 #2024 #nolimitdragracing2 #shorts
Persona 4 The Animation OP 1 - Sky's The Limit (TV Size) [1080p w/ Lyrics]
sky's the limit
Attitude - Lion King - Don't Cross The Limit 🦁 👑 #shorts #attitude #status #lionking
Kairi or jess no limit who is the god? #shorts #mlbb #mobilelegends #kairi #jessnolimit #viral
'Limit Yourself to One Person' #persona4golden
You’re a Star 🎬 ASMR Golden Era Hollywood #93
The rupee limit in Twilight Princess never made any sense #zelda
Комментарии
 0:08:57
0:08:57
 0:06:11
0:06:11
 0:14:59
0:14:59
 0:01:17
0:01:17
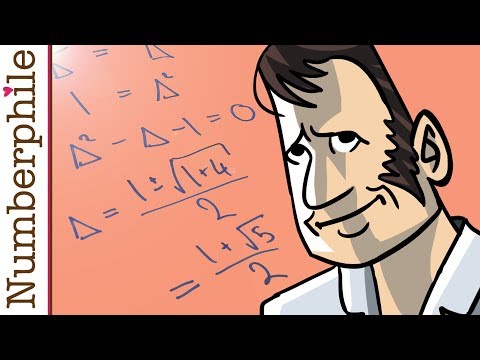 0:04:56
0:04:56
 0:10:04
0:10:04
 0:01:50
0:01:50
 0:03:50
0:03:50
 0:04:20
0:04:20
 0:04:02
0:04:02
 0:00:11
0:00:11
 0:07:31
0:07:31
 0:01:48
0:01:48
 0:00:41
0:00:41
 0:10:49
0:10:49
 0:04:12
0:04:12
 0:00:14
0:00:14
 0:01:31
0:01:31
 0:04:15
0:04:15
 0:00:17
0:00:17
 0:00:15
0:00:15
 0:00:51
0:00:51
 0:21:01
0:21:01
 0:00:23
0:00:23