Find Work Done By Adiabatic Process Using Calculus (Applied Calculus)

In this video we will be using calculus to prove the work formula
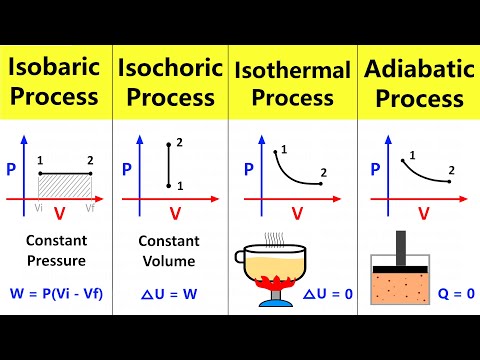
So we have a pressure and volume graph with and adiabat on it. The adiabatic process is where there is no heat transfer and pressure volume and temperature all change.
Below it 2 pistons that represent a change in volume.
We want to find the work done by this piston which is represented by the area under the adiabat curve
Recall that the ideal gas law for the adiabatic process is p1 times v1 to the power of gamma equals p2 times v2 to the power of gamma
Gamma being the ratio of the specific heat of a constant pressure process divided by the specific heat of a constant volume process. This can be found by looking up your value for the gas or subtstance you are working with. We will be using air and assuming a gamma of 1.41
So if we rearrange this formula to get pressure 2 to one side we get this equation
Really this equation is what is used to find the y or pressure value at any given point on this graph given you have a volume value
The 200 kilopascals time .1 meters cubed to the power of gamma will remain constant so to make it easier to look at lets replace all of those values with a K value
No we need to intergrate recal that dividing to a power is the same as multiplying that value to the negative power so we will do this to changing variable or delta volume
Using the power rule which basically you add 1 to the power then divide by the new power we just found we get this expression
Plugging in our K value and our volume of this problem we get the same value of work we previously found of 23,565 joules of work

Disclaimer
These videos are intended for educational purposes only (students trying to pass a class) If you design or build something based off of these videos you do so at your own risk. I am not a professional engineer and this should not be considered engineering advice. Consult an engineer if you feel you may put someone at risk.