How to Do the 1089 Number Trick | Magic Tricks

Rogue: Hey, Heather how you doing today?

Heather: Good, how are you?

Rogue: Good. Do you believe in psychic phenomenon?

Heater: I do.

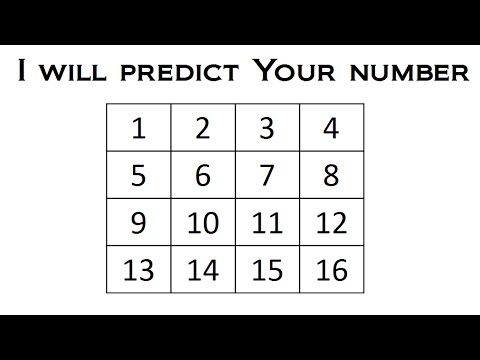
Rogue:You do, I'm sure you'd believe a cool demonstration of psychic phenomenon. I just need a number, I guess between one and a thousand, a three digit number.

Heather: Um, 642.

Rogue: 642. You wanna change your mind or that's a good number? 642. I'm gonna actually ask you now to randomize this number. What is the reverse of 642?

Heather: Um, 246.

Rogue: 246. All right, let's subtract these numbers.

Heater: 642. 246. 396.

Rogue: 396?

Heather: Yeah.

Rogue: Actually, let's randomize some more. What's the reverse for 396?

Heather: 693.

Rogue: 693. And instead of subtracting them let's add them together. What number do you have for that? 396, plus 693.

Heather: 1089. One thousand 89.

Rogue: One thousand eight-nine. Totally random number, would you say?

Heater: Yep.

Rogue: Well, it's crazy. Before this uh, trick started, I wrote (?) on the back from last night, it happens to be 1089. Isn't that great?

Heather: That's crazy.

Rogue: Totally crazy.

Basically what you're going to do is have your spectator name any three digit number. You can tell them that zero's a no good, not a real number, and don't repeat the numbers, so let's just try, like 123. It can be any three digit number like I said, three different numbers. And you're going tell them you're going to randomize the number. What you're going to do then is basically you're going to reverse the number that they just named, which is 321. And you're going to put the larger number on top of the smaller one and you're going to subtract that number so it's best to have somebody ready with a calculator. In this case let's do this. 198, you tell them, you know what, let's randomize it a little bit more, which you have to do for the trick to actually work, you're going to reverse the new number, 198, which is 891, and this you're going to add, so first subtract, then you're going to add the two numbers together. And believe it or not, you almost always, I would say 95-98 percent, it would equal 1089.

And you're probably asking, what's the other number it could be? I would say 2 percent of the time it's going to be the number 99, in which case, you never want to look silly when you're doing a trick for somebody, so I would actually put a paper in my pocket in plain view, just in one pocket so they don't think you have a bunch of predictions all over the place, that says you will pick the number 99, just in case the number turns out to be 99, which is a very slim chance, but it'll either equal 1089, most of the time, or equal 99. I want you to have fun with this, this is amazing, any time there's paper around, pens, you can do this illusion, anytime, anywhere. Have fun and that's called the 1089 trick.

[gchchung]

Let a, b and c be whole numbers (the digits) not equal to each other (he implies that in passing), let the three-digit number be expressed as 100a + 10b + c, and let a > c (he puts the larger number on top after reversing the digits). Given these conditions, the subtraction part of his routine will always give you a value of 99(a - c). For this number 99(a - c), the ones digit has a value of 10 + c - a (recall, a > c), the tens digit will always be 9, and the hundreds digit will always have a value of a - c - 1. You'll see immediately that the reversed-digit number of 99(a - c) has a value of 1089 - 99(a - c). For the addition part of the routine, you'll simply be adding 99(a - c) to 1089 - 99(a - c), which is just 1089, so it does not matter what 3-digit number you start with as long as the conditions above were met (no repeating digits). One possible complication happens when the first digit of the first (larger) number is only one more than the last digit (a = c + 1), then the subtraction part will give you 99. Then you'd need to tell your audience to work with 099 and add it to 990 to get back 1089.

[magicjack]

A comedic method is have the prediction upside down, which will be 6801. Most people won't notice it's 1089 inverted. Look at it, act embarrassed, then spin it around for success.

[s_patzz]

if you treat 99 as a 3 digit number (099) and add it to 990, it still works as 1089! THAT IS SUPERB!

[futurecomic]

fun fact, every number you get after subtracting the reverse is some multiple of 99. not only that, but the multiple is actually equal to the difference between the end numbers. for example 573-375=99×(5-3)

[masqueraderevelerss]

Wow, that's amazing. I tried it to my dad and it works!😀

[arisleongarcia]

OMG it works in tried it multiple times it works in love this and i impressed many of my friends 😊😊

[elliegarcia]

Dang, I'm not really into magic that much but i have some smart friends that get a kick out of this.

[TheLoobis]

Hey that's pretty cool. Just tried it on my self.

[Appelsnoes]

I took 132 and it gave 198... (99+99), but you should always write down the 3 digits, so say 099. That will give 099 + 990 = 1089

[mr.potato]

If you subtract the number and get a two digit number like 99 just change it to 099 then it will work.

[shivankpal]

Counterexample-
Take 786, reverse is 687 then 786 - 687 = 99 and then add reverse of 99 i.e. 99 + 99= 198.

[firstnamelastname]

There is another number 909


which can be the answer when all the digits different and the last digit as 0 or 9

[murukan]

really awesome you make my day wonderful Thank you very much

[reyparagas]

Try 563. It works and you are correct about that some numbers do not work.

[PugganBacklund]

if first and las number are the same, you can't reverse it, and therefore its end up as 0 insted of 1089, for all else you get 1089, true for 1-999 if you zero-pad your numbers to always be 3 digits, 900 combinations of 1089, and 99 of 0. if you don't zero-pad your number, the reversing give you smaller numbers, and when added you get smaller numbers, 64% end up as 1089, 17% end up as 198 (like 100 and 998, diff is 2 digits), 6% end up as 99 (like 13 and 97, startnumber and diff is 2 digits), and 1.7% as 18 (like 10 and 98, diff is 1 digit)

[melissama]

it works I tried 3 times it all worked. 1st: 765 2nd:381 3: 981

[drohegda]

Rogue I used to do this trick yeasr ago and i want to share a little twist i did on the trick, i would tell the person first to write down with pen and paper a three digit number on paper without me seeing and no zeros or double digits in the three digit number like you said.now when they finish the math i new the answer but i dont look at it, i said is you answer over a thousand, they said yes, before the trick i got a local phone book, white pages, and i told them what ever your last two digits, turn to that page in the book, which i new was 89 then i would say go to the far right column and count the number down of the first to digits in the answer, which i new was 10, and they'd go down and i would say please concentrate on the name, where i previously had looked and memorized the name, address, and phone # of the person, and would slowly as they concentrated tell them it all, and they would flip out in disbelief .just a little twist on you trick, thanks for the great video.my friend.drohegda

[firstnamelastname]

i know how to determin that it is 1089 or 99


if all the digits are diferent with no 0 the answer will definetly be 1089

However

if some or all of the digits are the same and if it has 0 or both the answer is 99

[wesleyw.terpstra]

The number 99 can only appear after the first subtraction step. If you write it down as 099, then adding 990 will still work. So the 675 case someone complained about would work like this.

For anyone who cares, this trick is easy to prove. Take your number 'xyz' (so if 431, x=4, y=3, z=1). So you start with (100*x + 10*y + z). Subtract (100*z + 10*y + x) to get 99*(x-z). Since duplicates are forbidden (x!=z) and you always write the bigger number on top, we know that 1 <= x-z <= 9. So let's call the result of subtraction just 99*k with 1 <= k <= 9. You can rewrite this as (k-1)*100 + 90 + (10-k). Add the reverse, (10-k)*100 + 90 + (k-1), and you will get 1089.

[Thrillseeker]

With 1089 pieces of paper in your pocket, you can always be right!