filmov
tv
Calculus: Easy Derivatives and Integrals Using Python
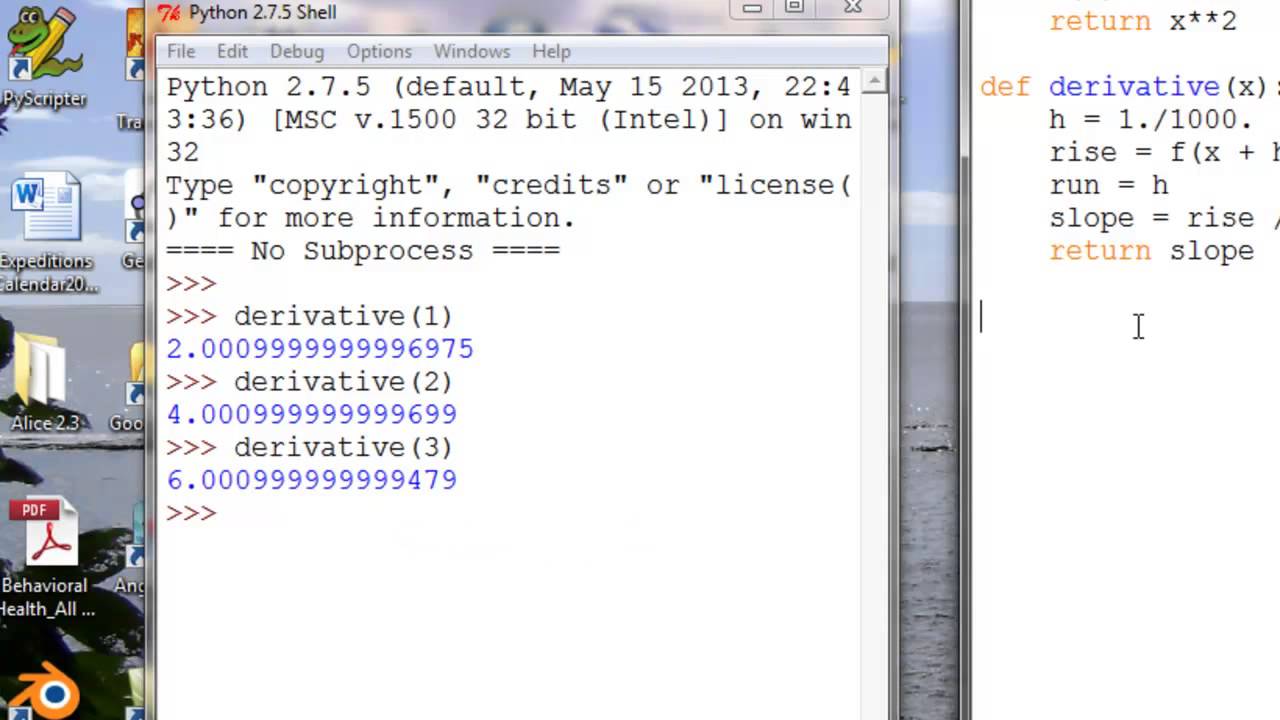
Показать описание
How to use Python to calculate the derivatives and integrals of functions. This program will get you the numerical values, but not the general function. But the computer does the hard work! Hope it helps you explore functions in Calculus.
Understand Calculus in 35 Minutes
Integration (Calculus)
Derivative as a concept | Derivatives introduction | AP Calculus AB | Khan Academy
Calculus 1 - Derivatives
Calculus 1 - Integration & Antiderivatives
Integration and the fundamental theorem of calculus | Chapter 8, Essence of calculus
Understand Calculus in 1 minute
Calculus in a nutshell
Integration the best ♥️. #viralvideo #maths #treadings #exam
Physics With Calculus - Basic Introduction
Understand Calculus in 10 Minutes
Introduction to integral calculus | Accumulation and Riemann sums | AP Calculus AB | Khan Academy
Calculus, what is it good for?
Calculus In Minecraft Terms | Integration & Differentiation (Calc 1)
Finding the Derivative of a Polynomial Function | Intro to Calculus #shorts #math #maths
Why is calculus so ... EASY ?
Math Integration Timelapse | Real-life Application of Calculus #math #maths #justicethetutor
Calculus Visualized - by Dennis F Davis
Differential Calculus- Explained in Just 4 Minutes
The essence of calculus
Calculus | Derivatives of a Function - Lesson 7 | Don't Memorise
Calculus - Definite Integrals
HOW TO READ CALCULUS OUT LOUD! | LIMITS, DERIVATIVES & INTEGRAL SYMBOLS
when calculus students use trig identities too early
Комментарии
 0:36:22
0:36:22
 0:07:04
0:07:04
 0:07:16
0:07:16
 0:52:51
0:52:51
 0:40:04
0:40:04
 0:20:46
0:20:46
 0:00:57
0:00:57
 0:03:01
0:03:01
 0:00:56
0:00:56
 0:14:07
0:14:07
 0:21:58
0:21:58
 0:04:52
0:04:52
 0:07:43
0:07:43
 0:04:18
0:04:18
 0:01:01
0:01:01
 0:38:32
0:38:32
 0:00:09
0:00:09
 3:00:44
3:00:44
 0:03:57
0:03:57
 0:17:05
0:17:05
 0:12:11
0:12:11
 0:07:15
0:07:15
 0:04:15
0:04:15
 0:00:43
0:00:43