filmov
tv
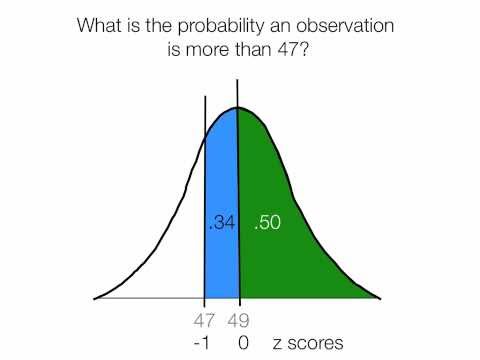
An example of how to calculate a z score.
Показать описание
z scores, statistics, probability
Logic: An Example of How to Kill A Rap Career
An example of How to use Ta-Da chair !
An example of how to use an Arise Standing wheelchair in the workplace.
An example of how to calculate a z score.
Example: How To Answer 'Tell Me About Yourself' at an Audition
An example of how to peel an apple #life
An example of how to solve an equation
The Game: An Example of How to Kill A Rap Career
We show an example of how to party properly
The six stroke roll is an example of how Travis Barker incorporates rudiments into blink-182’s music...
An example of how to calm a Tantrum | Calming a toddler tantrum
An example of how to use Matomo with chatgpt
Here is an example of how to set your pipeline parter up for success #welding #shorts
An example of how to use The Word 121
Is there an example of how to pray for someone who is sick?
Give The World The Best Example Of How To Love You | Lisa Nichols
How to Write an Example Paragraph
An Example of How to Add Two Polynomials
See caption or comments for an example of how to easily meet your protein needs! #proteingoals
Cesc Fabregas- An example of how to handle being dropped by Antonio Conte
Show your children an example of how to do things right 👍😁
How Anxiety Works: An Example
Here is an example of how to answer: what is your approach?
An Example of How to use Portainer to Control Kubernetes Environments in the Edge
Комментарии
 0:12:24
0:12:24
 0:00:40
0:00:40
 0:00:48
0:00:48
 0:05:31
0:05:31
 0:00:15
0:00:15
 0:03:41
0:03:41
 0:09:49
0:09:49
 0:00:10
0:00:10
 0:00:38
0:00:38
 0:00:49
0:00:49
 0:07:31
0:07:31
 0:00:26
0:00:26
 0:17:13
0:17:13
 0:01:32
0:01:32
 0:35:37
0:35:37
 0:15:19
0:15:19
 0:01:19
0:01:19
 0:00:58
0:00:58
 0:06:52
0:06:52
 0:00:18
0:00:18
 0:00:59
0:00:59
 0:01:00
0:01:00
 0:12:31
0:12:31