filmov
tv
Synthetic Division... How? (NancyPi)
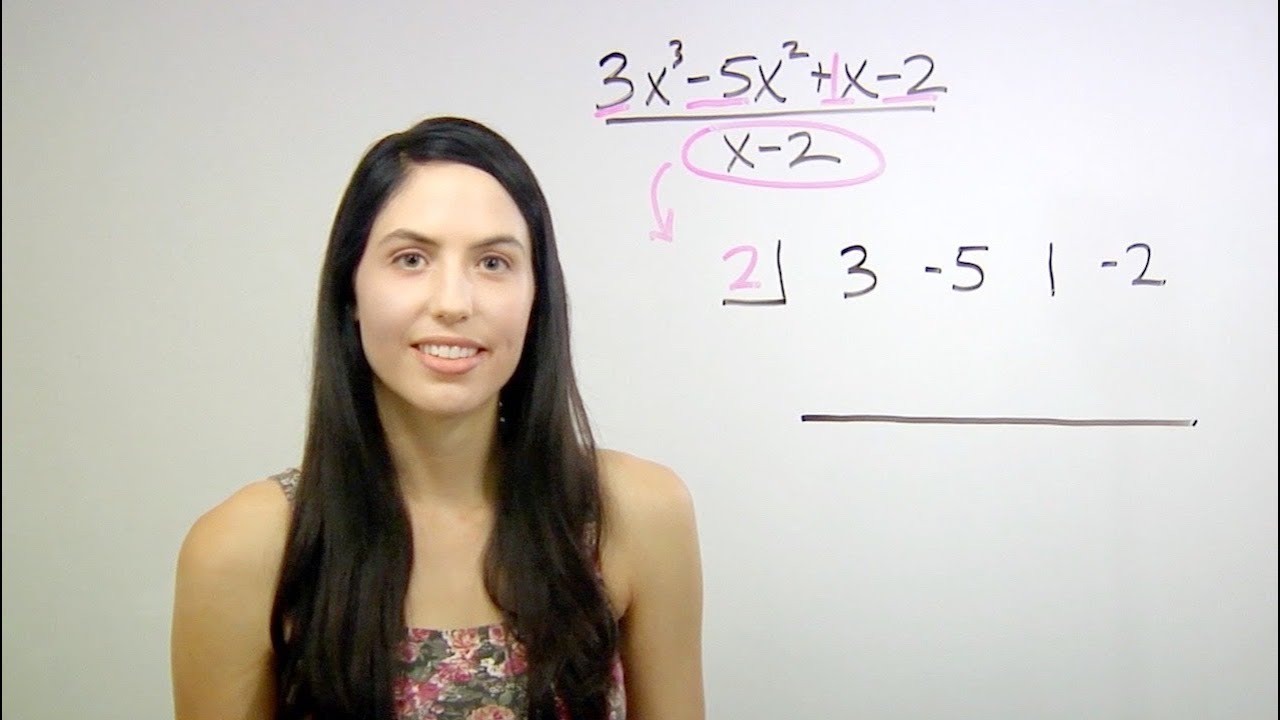
Показать описание
MIT grad shows how to do synthetic division, a shortcut for long division. It's a fast way of dividing polynomials, if you're dividing one polynomial by a linear expression like x+1 or x-3. To skip ahead: 1) For how to know WHICH NUMBERS to put in the corner of the division box and the first row, skip to time 0:22. 2) For the synthetic division STEPS of carrying down coefficients, multiplying, and adding, skip to 1:12. 3) For how to WRITE the FINAL ANSWER and how to WRITE the REMAINDER (if the last number you get is not zero, there is a remainder), skip to 3:37. 4) For what to do if you have a MISSING TERM and putting a zero as its placeholder, skip to 5:04. Nancy formerly of MathBFF explains the steps.
SYNTHETIC DIVISION is often faster than long division for dividing polynomials, if the polynomial you're dividing by is "x plus a number" or "x minus a number". It can be used to factor a polynomial and to find the zeros or roots of a polynomial.
HOW TO DO synthetic division of polynomials:
First draw a little corner symbol. Inside the corner, write the number that makes your denominator equal to zero. If your denominator is "x+1", you would write -1 in the corner. Then write the coefficients of your top polynomial in a row, to the right of the corner symbol. Leave space for another row and draw a horizontal line beneath that. Here are the steps to repeat for synthetic division, to carry down coefficient numbers, multiply, and add:
1) Drop down the first coefficient number.
2) Multiply this number by the corner constant.
3) Write the product in the second column, second row spot.
4) Add the two numbers in the second column, and write the sum below the line in the second column.
5) Repeat those steps until you have written a number in the final column spot below the line.
6) Write your new polynomial answer using this bottom row of numbers. The first number is the leading coefficient of your polynomial and is the coefficient of an x-term that is one degree less than your original polynomial. The second number is the coefficient of the second term, etc. For example, if the numbers are 1 4 3 2, the new polynomial is 1x^2 + 4x + 3 + 2/(x+1). Notice the last number is part of the remainder, so you write that number, 2, over the original divisor (x+1) as a fraction, for the remainder term.
Sometimes there is no remainder in synthetic division examples. If the last number you get is zero, in your final division numbers, then there is no remainder. Your final answer will just have a polynomial and no fraction term added at the end. Synthetic division is a way of factoring polynomials: if there is no remainder when you finish, you have found a true factor of the original polynomial. In the example above, if the remainder had been zero instead, the original polynomial would factor into (x+1)(x^2 + 4x + 3).
Note: also watch out for a missing term in your original polynomial: if there is no x-squared term, or no x term, etc, then in order to get the right answer for synthetic division, you will need to make sure to put a zero number in your first row of coefficient numbers, as a placeholder for that missing term.
SYNTHETIC DIVISION is often faster than long division for dividing polynomials, if the polynomial you're dividing by is "x plus a number" or "x minus a number". It can be used to factor a polynomial and to find the zeros or roots of a polynomial.
HOW TO DO synthetic division of polynomials:
First draw a little corner symbol. Inside the corner, write the number that makes your denominator equal to zero. If your denominator is "x+1", you would write -1 in the corner. Then write the coefficients of your top polynomial in a row, to the right of the corner symbol. Leave space for another row and draw a horizontal line beneath that. Here are the steps to repeat for synthetic division, to carry down coefficient numbers, multiply, and add:
1) Drop down the first coefficient number.
2) Multiply this number by the corner constant.
3) Write the product in the second column, second row spot.
4) Add the two numbers in the second column, and write the sum below the line in the second column.
5) Repeat those steps until you have written a number in the final column spot below the line.
6) Write your new polynomial answer using this bottom row of numbers. The first number is the leading coefficient of your polynomial and is the coefficient of an x-term that is one degree less than your original polynomial. The second number is the coefficient of the second term, etc. For example, if the numbers are 1 4 3 2, the new polynomial is 1x^2 + 4x + 3 + 2/(x+1). Notice the last number is part of the remainder, so you write that number, 2, over the original divisor (x+1) as a fraction, for the remainder term.
Sometimes there is no remainder in synthetic division examples. If the last number you get is zero, in your final division numbers, then there is no remainder. Your final answer will just have a polynomial and no fraction term added at the end. Synthetic division is a way of factoring polynomials: if there is no remainder when you finish, you have found a true factor of the original polynomial. In the example above, if the remainder had been zero instead, the original polynomial would factor into (x+1)(x^2 + 4x + 3).
Note: also watch out for a missing term in your original polynomial: if there is no x-squared term, or no x term, etc, then in order to get the right answer for synthetic division, you will need to make sure to put a zero number in your first row of coefficient numbers, as a placeholder for that missing term.
Комментарии
 0:06:35
0:06:35
 0:11:13
0:11:13
 0:06:37
0:06:37
 0:10:32
0:10:32
 0:03:25
0:03:25
 0:00:37
0:00:37
 0:04:46
0:04:46
 0:05:21
0:05:21
 0:24:14
0:24:14
 0:08:00
0:08:00
 0:12:56
0:12:56
 0:10:14
0:10:14
 0:02:19
0:02:19
 0:04:44
0:04:44
 0:06:42
0:06:42
 0:09:22
0:09:22
 0:52:49
0:52:49
 0:00:45
0:00:45
 0:00:36
0:00:36
 0:06:27
0:06:27
 0:05:43
0:05:43
 0:06:05
0:06:05
 0:03:51
0:03:51
 0:02:24
0:02:24