filmov
tv
An Interesting Trigonometric Equation

Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts).
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#algebra #counting #geometry #numbertheory #calculus
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#algebra #counting #geometry #numbertheory #calculus
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Trig Visualized: One Diagram to Rule them All (six trig functions in one diagram)
An Interesting Trigonometric Equation | Math Olympiads
An Interesting Trigonometric Equation
Solving an Interesting Trigonometric Equation
Solving Trigonometric Equations - How to Write General Solution
An Interesting Trigonometric Equation | Math Olympiads
Solving Trigonometric Equations By Finding All Solutions
Solving Trigonometric Equations By Factoring & By Using Double Angle Identities
Solving Trigonometric Equations (5 Examples)
Trigonometry Concepts - Don't Memorize! Visualize!
Solving Trigonometric Equations
An Introduction to Solving Trigonometric Equations
Solving Trigonometric Equations
Harder Trigonometric Equations
Trigonometry Angles Trick | Trigonometry Table #youtubeshorts #shorts #viralmaths #ashortaday #fun
How to Solve Trigonometric Equations (Precalculus - Trigonometry 22)
Trigonometry Formulas -2
Trigonometry Class 10 | Trigonometry Identities| Trigonometry Formulas #fun #shorts #youtubeshorts
Trigonometry is wasy
Easy Way to Remember Derivatives of Trigonometry Ratios #shorts | How to Remember Derivatives Easily
Day 20: Solving Trig Equations • 100 Days of A-Level Maths 🧮
(sinx)^5+(cosx)^7=1 | A Trigonometric Equation
How To Solve Trigonometric Equations With Multiple Angles - Trigonometry
Let's Solve A Cool Trigonometric Equation
Комментарии
 0:04:15
0:04:15
 0:10:16
0:10:16
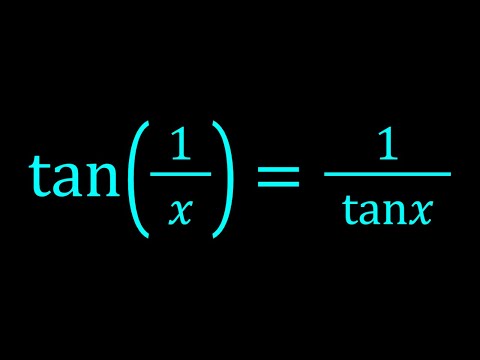 0:09:40
0:09:40
 0:09:06
0:09:06
 0:06:26
0:06:26
 0:09:31
0:09:31
 0:11:49
0:11:49
 0:18:32
0:18:32
 0:38:42
0:38:42
 0:32:35
0:32:35
 0:15:22
0:15:22
 0:14:17
0:14:17
 0:08:28
0:08:28
 0:12:41
0:12:41
 0:00:26
0:00:26
 1:34:36
1:34:36
 0:00:05
0:00:05
 0:00:14
0:00:14
 0:00:12
0:00:12
 0:00:50
0:00:50
 0:00:39
0:00:39
 0:06:06
0:06:06
 0:11:34
0:11:34
 0:09:17
0:09:17