filmov
tv
Calculus on the 3-sphere

Показать описание
Take these six steps in order to visualize three different types of path on S^3. First, parameterize a path by taking points from the line of Reals into the Complex plane. Second, use a map to take the path from the complex plane into the double struck C^2, which is the product of two complex planes. This type of path in C^2 is called gamma sub one. Third, solve a system of differential equations on C^2 in order to deform the path in a smooth way, without cutting it. This involves connecting a point in path gamma sub one to another point in the transformed version of gamma sub one. Do this for all of the points in gamma sub one and call the connecting paths gamma sub 2. Fourth, connect the endpoints of all paths of type gamma sub two in order to form the final version of transformed gamma sub one. Call the path made of the endpoints gamma sub three. Fifth, project all three types of path in C^2 to the three-dimensional unit sphere S^3 as a subset of C^2. Finally, by the Hopf map project all three types of path onto the two-dimensional unit sphere S^2 as a subset of double struck R^3, which is the Euclidean three-space.
Rupert Way (2008).
Rupert Way (2008).
Integration in Spherical Coordinates
Calculus 3 Lecture 11.7: Using Cylindrical and Spherical Coordinates
Calculus 3 Lecture 14.7: TRIPLE Integrals Over Regions with CYLINDRICAL or SPHERICAL Coord.
Calculus 3: Graphing in 3-D Basic Shapes (4 of 9) Equation of a Sphere
Multivariable Calculus | Triple integral with spherical coordinates: Example.
Calculus 3: Three-Dimensional Coordinate Systems (Video #1) | Math with Professor V
Intro to 3D Coordinates, Planes, and Spheres - CALCULUS 3
But why is a sphere's surface area four times its shadow?
The Volume of a Sphere - Numberphile
OpenStax Calculus 3 - 2.7 Cylindrical and Spherical Coordinates
Triple Integrals in Spherical Coordinates
Calculus 3 Lecture 11.6: Cylinders and Surfaces in 3-D
Calculus 3: Triple Integrals (5 of 25) Finding the Volume of a Semi-Sphere: Spherical
Calculus 1 - Derivatives and Related Rates (9 of 24) Growing Sphere
How To Find The Equation of a Sphere, Center, & Radius Given The Endpoints of its Diameter
Spherical Coordinates 3D Animation
But what is a partial differential equation? | DE2
Calculus 3: Triple Integrals in Spherical Coordinates (Video #25) | Math with Professor V
Divergence and curl: The language of Maxwell's equations, fluid flow, and more
Calculus 3: Triple Integrals (4 of 25) Choosing a Coordinate System: Spherical
The hardest problem on the hardest test
Calculus 3: Triple Integrals (24 of 25) Finding the Centroid: Center of Mass
Calculus III - Spheres and Ellipsoids
Triple Integrals - Calculus 3
Комментарии
 0:07:52
0:07:52
 1:40:16
1:40:16
 3:20:10
3:20:10
 0:02:24
0:02:24
 0:14:54
0:14:54
 0:31:42
0:31:42
 0:22:10
0:22:10
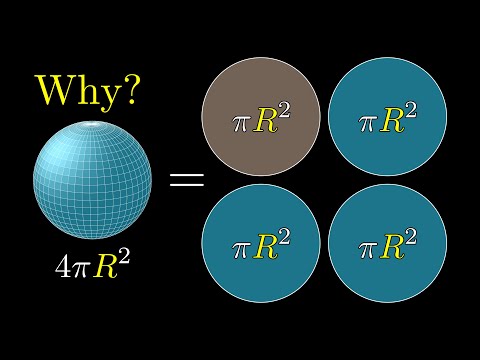 0:15:51
0:15:51
 0:04:14
0:04:14
 0:10:41
0:10:41
 0:28:43
0:28:43
 2:32:27
2:32:27
 0:05:22
0:05:22
 0:02:18
0:02:18
 0:11:48
0:11:48
 0:07:56
0:07:56
 0:17:39
0:17:39
 0:52:57
0:52:57
 0:15:42
0:15:42
 0:05:50
0:05:50
 0:11:15
0:11:15
 0:08:08
0:08:08
 0:20:44
0:20:44
 0:10:06
0:10:06