Topological Spaces Of Topological Space

My hope is that this video provides more evidence for my recent conjecture, about the presence of a particular type of metric that I tried to describe in my previous video
that can be defined on spaces of Frechet (V) spaces. In this video I look at simple two element examples, to build intuition,and then go through a rough argument for the presence of a natural metric upon the set of all Frechet spaces using the same elements.
A Frechet (V) space on a set K is where each element x of K is associated with a collection
of subsets of K, we refer these subsets as the neighbourhoods of x.
In the previous lecture
I made conjecture about a possible metric that could be defined on the set of all Frechet (V) spaces on set A.
Since the previous lecture I found a proof sketch for this idea, which I uploaded on to dropbox

Recently I have conjectured a new way to define the metric in terms of the minimum number of `neighbourhood replacement operations', required to convert on Frechet (V) space on K, into another. Taking this perspective, make it clear that the metric should satisfy the triangular inequality, as the hamming distance does. In important next step seems to be to get tactile information about the nature of this metric space on the space of Frechet spaces. What does it look like ? To start of answer this question I considered the simple case where we consider the four Frechet (V) space on {1,2} where points must be in their own neighbourhoods, and we consider how our metric is defined, giving a notion of distance between these four spaces, which can be visualised.

Using 1-hop graphs to visualise the entire metric space associated with the Frechet (V) spaces on set K={1,..,n} would be very interesting.

In addition to discussing theory, in this video I also examine some minimal cases of these spaces.

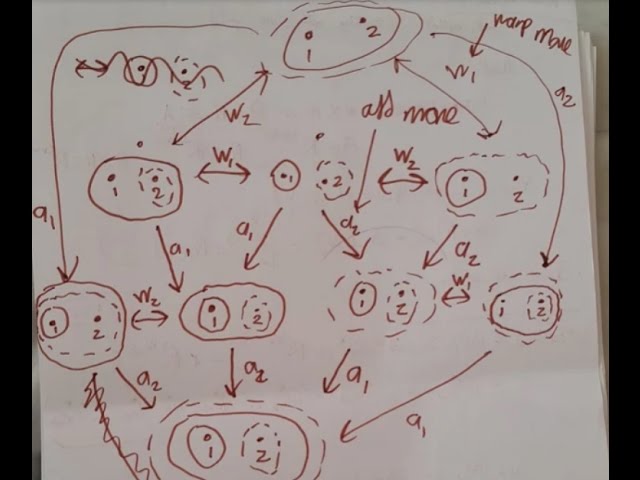
I illustrate the structure interrelating the nine Frechet (V) spaces on set {1,2} with the property that each neighbourhood of a point contains that point. Solid circles represent neighbourhoods of 1. Dashed circles represent neighbourhoods of 2. We show the one can convert between the spaces 'warp' operations, where we replace one neighbourhood with another, and 'add' operations where we add new neighbourhoods. The minimum number D (S,S') of these type of operations required to convert one Frechet V space S into another, S', seems to define a metric on this collection of Fechet V spaces, as I have discussed in my recent video about a potential example of a topological multiverse.

[RichardSouthwell]

Here is the pdf I read in the video
I try and prove the function D I defined was a metric space on the collection of Frechet (V) spaces which have the same set K of elements. Beware of typos etc. All this work has been done very quickly, and I have not had time to debug much,