filmov
tv
How to Solve Coupled Differential Equations ODEs in Python

Показать описание
Coupled System of Differential Equations
How to Solve Coupled Differential Equations ODEs in Python
Solving Coupled Differential Equations in Mathematica | Tutorial - 12
How to solve coupled differential equations?
How to Solve Differential Equations in PYTHON
IB MAI HL - 12.04.0 Coupled Differential Equations - Introduction
Solving Systems of Coupled Differential Equations (Part 1)
Modelling with Coupled Differential Equations | Mr Mathematics
Solution to Coupled Differential Equation Using Python
VO FA2 Week 21 2 Coupled differential equations
Coupled Ordinary differential equations using Maple
Differential equations, a tourist's guide | DE1
Solving a system of coupled, ordinary second-order differential equations
How to solve coupled differential equations, (Mathematica tutorials-02)
Systems of linear first-order odes | Lecture 39 | Differential Equations for Engineers
8: Eigenvalue Method for Systems - Dissecting Differential Equations
3 Coupled & Higher Order ODEs
NUPOC VSG #55 - Solving Coupled Differential Equations with Matrices
Coupled Linear Differential Equations
Matrix Systems of Differential Equations
Modelling with Differential Equations 7 • Coupled Differential Equations • CP2 Ex8D • 🏆
13FM - DE9 - Coupled differential equations
Solving Systems of Coupled Differential Equations (Part 2)
COUPLED DIFFERENTIAL EQN. VISUALISATION & MAKING MOVIE
Комментарии
 0:07:19
0:07:19
 0:10:12
0:10:12
 0:07:54
0:07:54
 0:03:13
0:03:13
 0:23:37
0:23:37
 0:04:59
0:04:59
 0:55:06
0:55:06
 0:09:40
0:09:40
 0:12:25
0:12:25
 0:35:15
0:35:15
 0:14:06
0:14:06
 0:27:16
0:27:16
 0:15:18
0:15:18
 0:05:33
0:05:33
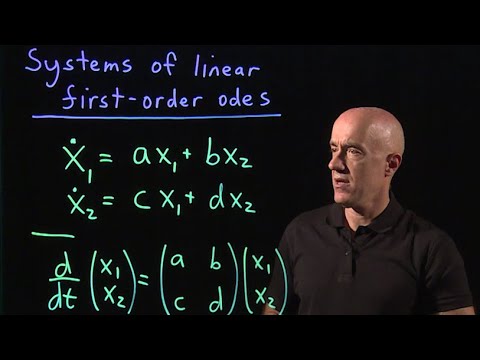 0:08:28
0:08:28
 0:08:57
0:08:57
 0:12:11
0:12:11
 0:00:58
0:00:58
 0:05:41
0:05:41
 0:24:58
0:24:58
 0:38:24
0:38:24
 0:14:27
0:14:27
 0:29:07
0:29:07
 0:44:26
0:44:26