filmov
tv
How to find the area of a triangle inside of a rectangle

Показать описание
We are given the area of the rectangle is 96 and we know two parts are 5 and 8, as indicated on the picture. We need to find the area of the shaded triangle. I will present the easiest solution to solve this tricky geometry puzzle!
-----------------------------
-----------------------------
#math #algebra #mathbasics
-----------------------------
-----------------------------
#math #algebra #mathbasics
Finding the Area of a Composite Figure | Area of Composite Rectangles
Math Antics - Area
How to Find the Area of a Rectangle | Math with Mr. J
How to Find Area | Rectangles, Squares, Triangles, & Circles | Math Mr. J
Area of a triangle #area #maths #mathsrevision
Area for Kids
How to Find the Area of a Square | Math with Mr. J
Area of the figure | Area of the rectangle | #mathstricks #shorts
Area and Perimeter of a Square Explained
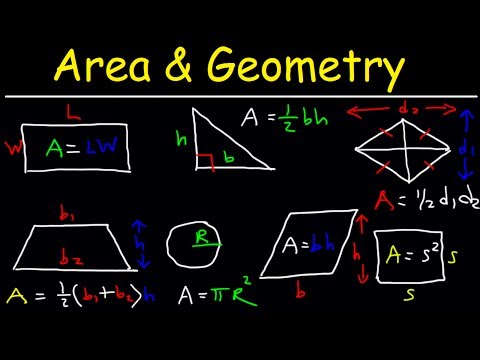
Area of a Rectangle, Triangle, Circle & Sector, Trapezoid, Square, Parallelogram, Rhombus, Geome...
How to Find the Area of a Circle | Area of a Circle Step by Step
Area & Perimeter of a Triangle
How to find Area of square #maths #shorts
How To find Area of CIRCLE? #shorts #maths
How to Find the Area of a Triangle | Calculate the Area of a Triangle
Finding the Area of a Triangle | A Step-By-Step Guide | Math with Mr. J
Area and Perimeter
Calculating the Area of Shapes
How to find Area Of Sector. (DONT MISS OUT)! #viral #maths
Area of a Circle | MathHelp.com
Area of a Trapezoid (Trapezium) | Math with Mr. J
GCSE Maths - How to Find the Area of Rectangles, Parallelograms, Triangles and Trapeziums
How to Find Area and Perimeter | Educational Rap for Math Curriculum
How to Find the Area of a Circle | Math with Mr. J
Комментарии
 0:07:14
0:07:14
 0:10:26
0:10:26
 0:04:43
0:04:43
 0:22:11
0:22:11
 0:00:33
0:00:33
 0:08:58
0:08:58
 0:02:48
0:02:48
 0:00:48
0:00:48
 0:10:53
0:10:53
 0:20:35
0:20:35
 0:06:39
0:06:39
 0:00:16
0:00:16
 0:00:23
0:00:23
 0:00:16
0:00:16
 0:06:37
0:06:37
 0:07:35
0:07:35
 0:17:49
0:17:49
 0:06:39
0:06:39
 0:00:16
0:00:16
 0:01:40
0:01:40
 0:06:14
0:06:14
 0:05:32
0:05:32
 0:03:26
0:03:26
 0:09:08
0:09:08