Polynomial Synthetic Division [A fifth Example:]

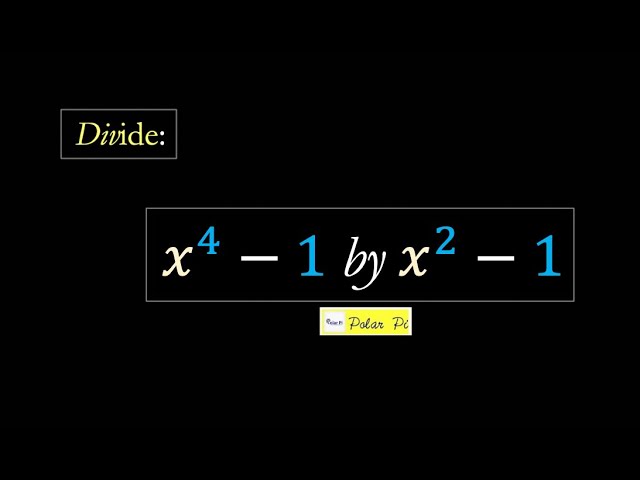
preview_player
Показать описание
Here is an example on dividing by a factorable quadratic through repeated application of Synthetic Division [in other words, going around the handicap of Synthetic Division.]

Jesus Christ God is NOT white and spoke clearly about being a "jealous God" and more importantly about all forms of image worship, but if you want to continue to offend God and live with the consequences, I will cease to remind you after this video.
  1. Polar Pi
  2. polynomial synthetic division
  3. synthetic division of polynomials
  4. how to divide polynomials
  5. polynomial division
  6. easy polynomial division using synthetic division
Рекомендации по теме
Synthetic Division of 0:10:32

Synthetic Division of Polynomials

Polynomial Synthetic Division 0:05:26

Polynomial Synthetic Division [A fifth Example:]

Solving Higher-Degree Polynomials 0:09:22

Solving Higher-Degree Polynomials by Synthetic Division and the Rational Roots Test

Solve a 5th 0:05:11

Solve a 5th degree polynomial equation using synthetic division.

Divide a Fifth 0:05:52

Divide a Fifth Degree Polynomial by a Binomial Using Synthetic Division

Dividing a Polynomial 0:05:47

Dividing a Polynomial by a Trinomial Using Synthetic Division

Why synthetic division 0:07:00

Why synthetic division works | Polynomial and rational functions | Algebra II | Khan Academy

Applying synthetic division 0:02:03

Applying synthetic division to a polynomial with missing terms

How To Factor 0:00:39

How To Factor a Polynomial to the 5th Degree #shorts

Using Synthetic Division 0:04:03

Using Synthetic Division to Evaluate a Polynomial

Dividing Polynomials Using 0:03:48

Dividing Polynomials Using Synthetic Division: Ex 3

Dividing Polynomials by 0:10:54

Dividing Polynomials by Synthetic Division - Polynomial Division - Grade 10

Long Division With 0:12:12

Long Division With Polynomials - The Easy Way!

Precalculus - Factoring 0:17:22

Precalculus - Factoring Higher Order Polynomials - Synthetic Division

Polynomial Synthetic Division 0:09:52

Polynomial Synthetic Division

All Zeros of 0:07:28

All Zeros of a fifth degree Polynomial Function

Dividing polynomials- synthetic 0:07:03

Dividing polynomials- synthetic division

Polynomial Division: Synthetic 0:10:07

Polynomial Division: Synthetic Division

Synthetic Division Dividing 0:07:42

Synthetic Division Dividing by a Cubic

Algebra 2 Lesson 0:22:17

Algebra 2 Lesson #38 Dividing Polynomials Using Synthetic Division

Synthetic Division and 0:52:49

Synthetic Division and Long Division of Polynomials (Precalculus - College Algebra 32)

How to Divide 0:10:50

How to Divide Polynomials with Quadratic Divisor | SYNTHETIC DIVISION || LMT101

Factoring a Polynomial 0:03:31

Factoring a Polynomial using Synthetic Division

How to factor 0:07:44

How to factor a 5-term polynomial (rational zero theorem & synthetic division)

Комментарии
Автор

Take requests? I don't get partial derivatives. Do (x+i*y)^n or some of these. My education is grade 12 pre-cal completed. I don't have anything after that.

Ellipse Positive Set, x^2+x*y+y^2=1, <(1/3)*sqrt(3)*cos(ϑ)-sin(ϑ),
[x/sqrt(x^2+x*y+y^2), y/sqrt(x^2+x*y+y^2)]
[(x^2-y^2)/(x^2+x*y+y^2), y*(y+2*x)/(x^2+x*y+y^2)]
[(x^3-3*x*y^2-y^3)/(x^2+x*y+y^2)^(3/2),
[(x^4-6*x^2*y^2-4*x*y^3)/(x^2+x*y+y^2)^2,
[(x^5-10*x^3*y^2-10*x^2*y^3+y^5)/(x^2+x*y+y^2)^(5/2),

Ellipse Negative Set, x^2-x*y+y^2=1, <cos(ϑ)-(1/3)*sqrt(3)*sin(ϑ),
[x/sqrt(x^2-x*y+y^2), y/sqrt(x^2-x*y+y^2)]
[(x^2-y^2)/(x^2-x*y+y^2), y*(-y+2*x)/(x^2-x*y+y^2)]
[(x^3-3*x*y^2+y^3)/(x^2-x*y+y^2)^(3/2),
[(x^4-6*x^2*y^2+4*x*y^3)/(x^2-x*y+y^2)^2,
[(x^5-10*x^3*y^2+10*x^2*y^3-y^5)/(x^2-x*y+y^2)^(5/2),

thomasolson