Projection operators in quantum mechanics

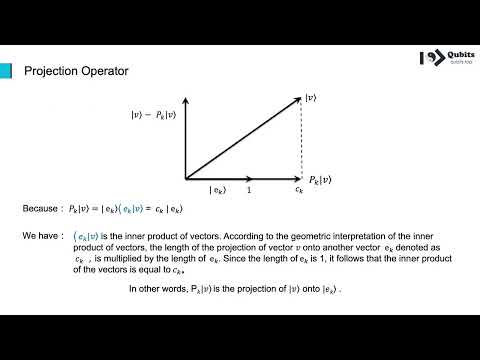
📚 In this video we learn about the properties of the projection operator in quantum mechanics. The projection operator allows us to find the component of a quantum state along another quantum state or within a subspace of the full state space. It finds applications in many areas, ranging from what happens to the state of a particle after we perform a measurement of one of its properties, to the construction of the symmetric and antisymmetric states under particle exchange that describe quantum systems of multiple identical particles.

⏮️ BACKGROUND

⏭️ WHAT NEXT?

~
Director and writer: BM
Producer and designer: MC

[anthonycortez]

What a gem!! Glad I found this channel! I'll be back.

[Lyxtwa]

I was reading Griffiths explanation of the projection operator and I had no idea how the inner product was moved in front of the ket. It was a very simple realization, but you helped me realize that any inner product is a scalar which can trivially be moved in front of the ket and probably saved me hours of confusion. Thank you so much.

[zonglangfrancis]

Thanks a lot for this vivid description of the projection operator.

[supergravity]

Another presentation that displays clarity, completeness and accuracy! Keep it up!

[musictoonz]

This is an amazing video than others available on youtube.
Thank you so much for this video

[attilauhljar]

Super clear and easy to follow explanation, very helpful, thanks. Keep up the god work!

[jayjain]

Thank you so much, I didn't know QM could be taught this nicely

[mehanaziqbal]

You’re a lifesaver.
Can’t thank you enough for these great videos😊.
Can you please make videos on Electrodynamics?😢

[hollywoodbanayad]

What a rich video, thank you so much for sharing

[qubit]

Good explanation, easy to understand. Thanks sir!👍👍👍

[nomanahmadkhan]

I have few questions.
1- I can see intuitively that eigenvalues of P are 0 and 1. But let me re-write the equation at 4:28
lambda|lambda>=c|psi>
lambda<psi|lambda>=c
lambda c=c
lambda=1
How do we get lambda=0 exactly?
2- Projection operator is hermitian and it has two eigenvalues as well as two eigenstates. So its matrix form in the basis of its eigenstates is a 2*2 diagonal matrix with diagonal entries 1 and 0, am I right?
3- Spin also has two eigenvalues 0 and 1, so is it also a projection operator? (Anxiously waiting for your video on spin!)
4- Since basis of a state space is not unique so can there be more than one pairs of complementary spaces?

[yashodabhattarai]

This is very helpful video 👏 Thank you very much 👌

[nourelhudazuraiki]

Thank you so much. This was very helpful. Just why is the projection operator for a ket is the outer product of the ket with itself?

[williamberquist]

at 9:30, is the projective operator P_m or P_n? It seems like you are saying P_n and it makes sense it would be P_n given we are working on an n-dimensional subspace. However, it looks like you wrote P_m. Is that just a fancy cursive n?

[aidenigelson]

Greetings. May I ask how we can project the system state from a 3 basis subspace to a 5 basis subspace and vice versa? I am trying to understand how mathematically we can (if possible) do the projection of the system state in a sequential incompatible observable projection, where we have two incompatible states, one is in 3 basis, the other in 5. How can we project the state sequentially from one onto the other? I understand the mathematics for the same dimension scenario, but wish to be sure regarding the generalized approach of any two arbitrary dimension subspace observable.
I would be immensely grateful for any guidance

[jzl]

This was an amazing video, thank you so much! I understood a lot more leaving than coming =] 

I feel like this might be a basic question, but intuitively, why can any arbitrary vector be represented as a sum of parallel/perpedicular vectors to another vector?

[syedanaushabinzakirkhanp]

What about the operator (X+iY) where X and Y are Pauli spin operators. It's not a projection operator as (X+iY)²=0, it has real eigenvalue, but isn't a Hermitian operator as (X+iY)†≠(X+iY). I'm not sure if it's unitary (I don't think it is). Then what kind of operator is it? Is it even a valid operator?

[tomaskubalik]

1) Do we know before measurement onto which subspace will the vector (quantum state) from V be projected or do we just know the probability that the vector will be projected onto subspace V1 and probability it will be projected onto V0? 2) Do I get identity operator if I put together all projection operators? 3) Can we use identity operator to project vector (quantum state) from V onto itself? Can V be its own subspace? Thanks

[enricolucarelli]

You have proved that the projection operator is Hermitian. You also proved in another video that any Hermitian operator has always n eigenvectors with all its eigenvalues real, and that this set of n eigenvectors form a full orthonormal base of the vector space.Thus, I thing that the interpretation I understand of your proof regarding the eigenvectors of a projection operator is to say that: the protection operator on |psi> has one eigenvector which is the actual vector |psi>, and the remaining n-1 eigenvectors are necessarily orthogonal to |psi>. The solution lambda = 0 represents the n-1 eigenvectors that are perpendicular to |psi>, but they are to be found by the classical procedure.
Please correct me if I am mistaken.

[jsconventschooldallaobraso]

Sir explain sign used in this method easily or make another video