filmov
tv
Integral of absolute value of x (abs x)

Показать описание
In this video we're finding the Integral of absolute value of x (abs x). Enjoy!
#math #brithemathguy #integral
►BECOME A CHANNEL MEMBER
Disclaimer: This video is for entertainment purposes only and should not be considered academic. Though all information is provided in good faith, no warranty of any kind, expressed or implied, is made with regards to the accuracy, validity, reliability, consistency, adequacy, or completeness of this information.
#math #brithemathguy #integral
►BECOME A CHANNEL MEMBER
Disclaimer: This video is for entertainment purposes only and should not be considered academic. Though all information is provided in good faith, no warranty of any kind, expressed or implied, is made with regards to the accuracy, validity, reliability, consistency, adequacy, or completeness of this information.
Definite Integral with Absolute Value |2x - 7| from 0 to 7/2
Integral of absolute value of x or abs(x)
Absolute Value Integrals
Definite integral of absolute value function | AP Calculus AB | Khan Academy
Definite Integral with Absolute Value (Example)
Evaluate the definite integral with absolute value
Integral of abs(x) in 44 seconds!
Absolute value integral
Integral of tan(x)dx
How to evaluate the definite integral with absolute value
Definite Integral of the Absolute Value of x from -1 to 2
Evaluating Definite Integral with Absolute Value
Integral of The Absolute Value of Sine from 0 to 3pi/2
Definite Integral with Absolute Value
Definite Integral of an Absolute Value Function ❖ Calculus
Learn how to evaluate the definite integral of absolute value by graphing
Ex: Definite Integration of an Absolute Value Function Using Geometric Formula
Setting Up Definite Integral of Absolute Value Function
Evaluating the integral of an absolute value function
The Integral and Derivative of an Absolute Value
The TRUE Integral of |x|, the absolute value. | Shorts
How to evaluate the definite integral of absolute value
Integrals involving absolute value function - Integral of Absolute value - Calculus
Absolute Value Definite Integral - Example 1
Комментарии
 0:04:44
0:04:44
 0:01:59
0:01:59
 0:13:26
0:13:26
 0:06:52
0:06:52
 0:07:17
0:07:17
 0:03:00
0:03:00
 0:00:44
0:00:44
 0:16:09
0:16:09
 0:02:23
0:02:23
 0:04:33
0:04:33
 0:03:02
0:03:02
 0:03:16
0:03:16
 0:04:51
0:04:51
 0:08:25
0:08:25
 0:05:23
0:05:23
 0:02:22
0:02:22
 0:04:21
0:04:21
 0:03:06
0:03:06
 0:08:55
0:08:55
 0:06:26
0:06:26
 0:01:00
0:01:00
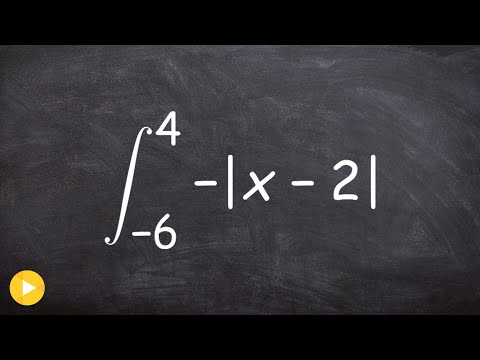 0:04:18
0:04:18
 0:29:00
0:29:00
 0:10:36
0:10:36