Prove that |Z1+Z2|≤ |Z1|+|Z2| and |Z1+Z2|≥ ||Z1|-|Z2|| for Complex Numbers

preview_player
Показать описание

Hi! In this video, I have proved two important inequalities from the complex number---- |Z1+Z2|≤ |Z1|+|Z2| and |Z1+Z2|≥ ||Z1|-|Z2||. Please watch the full video.

The same relation holds true for vectors also. Please watch the following video.

Hey! I have made this video using the Samsung Galaxy S6 tab. It's highly recommended to use. If you are a grad student you can have this pocket-friendly one. You can use a cool keyboard alongside, which will facilitate ease of working.

Books I recommend for Complex Analysis:
1) Complex Variable (Schaum's Outlines) |Revised 2nd Edition by M.R. Spiegel
2) Higher Engineering Mathematics by B. S. Grewal
3) Mathematical Physics by P. K. Chattopadhyay
  1. Ayan Sarkar
  2. complex number
  3. swartz inequality
  4. complex number inequality prrofs
  5. complex number identities
  6. Prove that |Z1 Z2|≤ |Z1| |Z2| and |Z1 Z2|≥ ||Z1|-|Z2|| for Complex Numbers
Рекомендации по теме
Prove that |Z1+Z2|≤ 0:11:00

Prove that |Z1+Z2|≤ |Z1|+|Z2| and |Z1+Z2|≥ ||Z1|-|Z2|| for Complex Numbers

How to prove 0:11:32

How to prove that (z1+z2)/(z1-z2) is purely imaginary when |z1|=|z2| using geometrical means

2. Find the 0:05:12

2. Find the greatest and least values of |Z1+Z2| or Prove that |z1+z2|≤|z1|+|z2| | AdnanAlig

|z1z2| = |z1||z2| 0:04:25

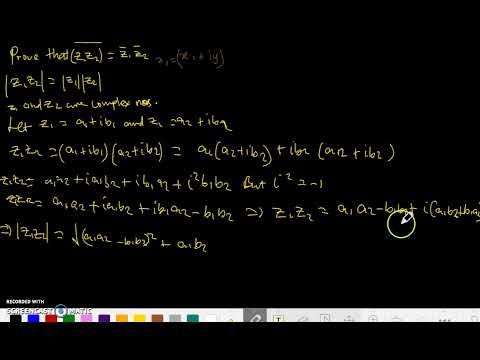
|z1z2| = |z1||z2|

Properties of Conjugate 0:13:51

Properties of Conjugate Complex Numbers | Complex no | Conjugate Complex Numbers | Trignometry

5.Find the greatest 0:23:14

5.Find the greatest and least values of |Z1+Z2| or Prove that ||z1|-|z2||≤|z1+z2|≤|z1|+|z2|

proof of modulus 0:13:02

proof of modulus property## mod of（ Z1/Z2 ）= （modZ1）/（modZ2）# Youtubevideo

Math's|Class #9th |Ch 0:17:13

Math's|Class #9th |Ch #1|Ex # 1.6|Q#5 (i &ii)|Sindh Textbook Board

Prove |z1+z2|^2+|z1-z2|^2=2(|z1|^2+|z2|^2) for 0:04:04

Prove |z1+z2|^2+|z1-z2|^2=2(|z1|^2+|z2|^2) for any Complex no | Properties of Complex Numbers

Prove |z1+z2+z3|^2+|-z1+z2+z3|^2+|z1-z2+z3|^2+|z1+z2-z3|^2=4[|z1|^2+|z2|^2+|z3|^2]. 0:09:51

Prove |z1+z2+z3|^2+|-z1+z2+z3|^2+|z1-z2+z3|^2+|z1+z2-z3|^2=4[|z1|^2+|z2|^2+|z3|^2].

Prove that |z_1+z_2 0:11:43

Prove that |z_1+z_2 |^2= |z_1 |^2+|z_2 |^2+2Re(z_1 z_2^* ) Complex Numbers Modulus Properties

PROVE /Z1Z2/ =/Z1//Z2/ 0:15:02

PROVE /Z1Z2/ =/Z1//Z2/

6. Prove that 0:11:05

6. Prove that |z1+z2|^2+|z1-z2|^2=2(|z1|^2+|z2|^2) for complex numbers z1 and z2

Conjugate the values 0:17:43

Conjugate the values and prove that Z1+Z2 = Z1+Z2

If z1, z2 0:01:39

If z1, z2 are two complex numbers such that |z1 + z2| = |z1 – z2| then amp(z1) –...

If z1,z2 be 0:01:00

If z1,z2 be two complex numbers such that z1/z2+z2/z1=1,prove that z1, z2, origin forms equilateral

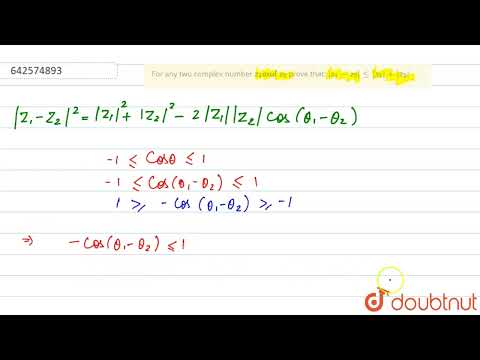
For any two 0:03:11

For any two complex numbers z1 and z2, prove that |z1 - z2| is less than equal to |z1| + |z2|

#proof of modulus 0:01:01

#proof of modulus property mod ( Z1/Z2 ）= （modZ1）/（modZ2) #shorts #class11th #@deeptirathore!!...

Prove that |1 0:05:07

Prove that |1 - z1*conjugate(z2)|^2 - |z1 - z2|^2 = [1 - |z1|^2][1 - |z2|^2].

Triangle Inequality for 0:06:55

Triangle Inequality for Complex Numbers

#math#inter2a#prove #conj(Z1+Z2)=? 0:01:00

#math#inter2a#prove #conj(Z1+Z2)=?

proof of mod(Z1.Z2) 0:01:01

proof of mod(Z1.Z2) = mod(Z1).mod(Z2) !@ #maths #youtubeshorts #shorts #short #trick #modulus

Triangle Inequalities of 0:12:18

Triangle Inequalities of complex numbers|proof of triangle inequities|Complex numbers

If z_1 and 0:01:10

If z_1 and z_2 be any two complex numbers such that |z_1+z_2 |=|z_1 |+|z_2 |, then arg〖 z〗_1-arg

Комментарии
Автор

From Vietnam:
Can you tell me under what circumstances the equal sign of that inequality occurs?
Hope for your answer

kietngo
Автор

The second equation if it's | Z1-Z2| And the right-hand side is the same as how it can be solved.

farahmohammad
Автор

2:19 Don't understood how he write z₁z₂*+z₁*z₂

Chinmoy-Saha