filmov
tv
The meaning of the dot product | Linear algebra makes sense

Показать описание
This video explains why the dot product is about how much vectors point the same way.
The meaning of the dot product | Linear algebra makes sense
The Dot Product - A Visual Explanation
Dot | Meaning of dot
DOT Meaning
Dot Meaning
Dot Meaning
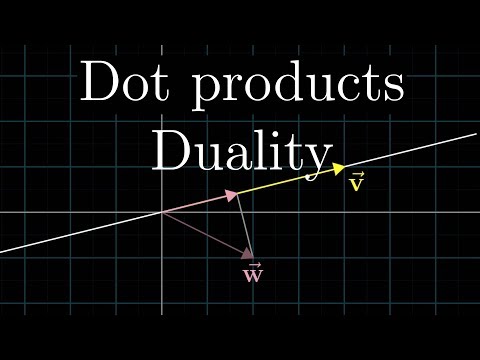
Dot products and duality | Chapter 9, Essence of linear algebra
The Dot Symbol | What Is The Spiritual Meaning Of A Dot? |
What Is The History Between 50 Cent And P Diddy?🤔 #raplifestyle #hiphopmusic
🟠 International Dot Day for Kids | 15 September | The meaning behind Dot Day | Twinkl USA
Dot Product (1 of 2: Geometric interpretation)
What Does The Red Dot On An Indian's Forehead Mean?
The real world applications of the dot product
Meaning of dot product
Cross Product and Dot Product: Visual explanation
The Vector Dot Product
Dot dot dot Meaning
How to Find the Mean from a Dot Plot | Math with Mr. J
Dot meaning in Hindi | Dot ka kya matlab hota hai | daily use English words
Full Form of DOT | DOT full form | DOT Ka Full Form | DOT Stands for | DOT Means | #Shorts_Video
iPhone: The New Privacy ‘Orange Dot’ You Need to Know About
what is the meaning of these colour Mark on product ? | Red Dot | Green Dot | Knowledge conscious
What Does The Green Dot Mean On Android?
What Does a Dot Do to a Note in Music?
Комментарии
 0:13:04
0:13:04
 0:01:50
0:01:50
 0:02:38
0:02:38
 0:00:22
0:00:22
 0:00:21
0:00:21
 0:00:51
0:00:51
 0:14:12
0:14:12
 0:02:17
0:02:17
 0:00:42
0:00:42
 0:02:48
0:02:48
 0:15:14
0:15:14
 0:00:53
0:00:53
 0:12:49
0:12:49
 0:06:24
0:06:24
 0:04:08
0:04:08
 0:06:59
0:06:59
 0:00:25
0:00:25
 0:05:09
0:05:09
 0:00:43
0:00:43
 0:00:18
0:00:18
 0:01:58
0:01:58
 0:01:19
0:01:19
 0:02:24
0:02:24
 0:03:44
0:03:44