Differential Equations: Logistic Equation: Analytic Solution

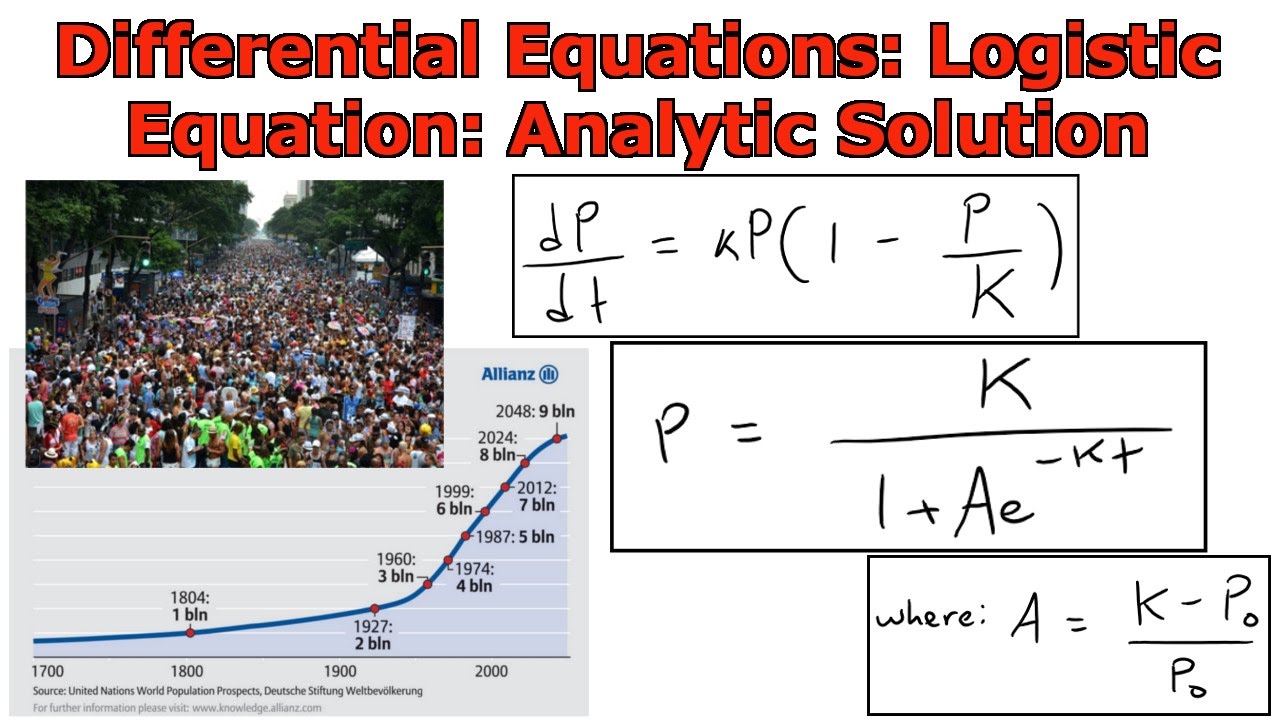
In this video I go over the derivation of the analytic or explicit solution of the logistic differential equation for modeling population growth. The logistic equation is separable which makes it possible to solve the explicitly. In the derivation, I integrate using the method of partial fractions, so this video is a good refresher on that method as well. This solution, and its derivation is a very important mathematical model for population growth, so make sure to watch this video!

Related Videos:

------------------------------------------------------

[mes]

I don't always model population growth but when I do I usually use the explicit solution of the logistic equation ;)

[sharifahmed]

Thanks prof for this upload. Please expand your channel, and it will be very helpful resource for students ODE.