filmov
tv
Solving an Exponential Diophantine Equation

Показать описание
This video is about solving an Exponential Diophantine Equation
If you need to post a picture of your solution or idea:
#NumberTheoryProblems #DiophantineEquations
EXPLORE:
If you need to post a picture of your solution or idea:
#NumberTheoryProblems #DiophantineEquations
EXPLORE:
I Solved An Exponential Diophantine Equation
A Surprisingly Easy Exponential Diophantine Equation to Solve in Algebra - Math Olympiad
Solving an Exponential Diophantine Equation
Solving an Exponential Diophantine Equation
an exponential Diophantine equation.
This Exponential Diophantine Equation Is Usually Solved Using Number Theory
Solving an Exponential Diophantine Equation
Solving a Diophantine Equation (3^x-2^y=1)
Use modular arithmetic to solve an exponential Diophantine equation: 7^x=3*2^y+1
An exponential Diophantine equation
Exponential equation | How To Solve Diophantine Equations | Diophantine Equations.
EXPONENTIAL DIOPHANTINE EQUATIONS PART1
An Exponential Diophantine Equation | Number Theory
a nice exponential Diophantine equation -- #maths
The Coolest Exponential Diophantine Equation from Dutch Math Olympiad
A Quick and Easy Solution to Diophantine Exponential Equation
How to Solve the Exponential Diophantine Equation 2^a+4^b+8^c=328? | Integer Solution
Math Olympiad | An Exponential Diophantine Equation #maths
How To Solve An Exponential Diophantine Equation #numbertheoryproblems #numbertheory
The making of an exponential Diophantine equation.
Solve For Positive Integers | Solving a Nice Exponential Diophantine Equations
US- A Nice Exponential Diophantine Equation#mathematics #matholympiadproblems
Solving a Diophantine Equation by Factoring | Solve for Integer Solutions #NumberTheory
Solve Diophantine Equations by Factoring
Комментарии
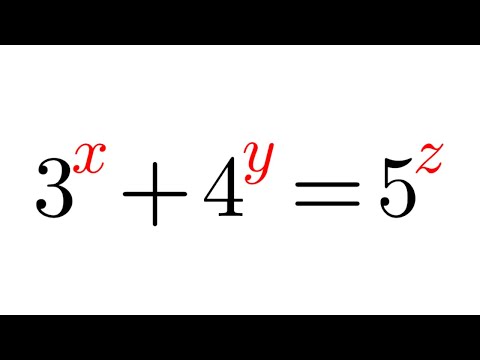 0:11:12
0:11:12
 0:05:54
0:05:54
 0:05:31
0:05:31
 0:05:31
0:05:31
 0:16:38
0:16:38
 0:11:27
0:11:27
 0:09:23
0:09:23
 0:07:41
0:07:41
 0:08:07
0:08:07
 0:14:06
0:14:06
 0:10:47
0:10:47
 0:06:04
0:06:04
 0:11:02
0:11:02
 0:00:54
0:00:54
 0:04:20
0:04:20
 0:07:44
0:07:44
 0:03:52
0:03:52
 0:03:19
0:03:19
 0:00:26
0:00:26
 0:10:49
0:10:49
 0:04:10
0:04:10
 0:06:42
0:06:42
 0:07:08
0:07:08
 0:01:58
0:01:58