Hypothesis Testing: Critical values & Rejection Regions I Statistics 101 #4 | MarinStatsLectures

Hypothesis Testing 4: Critical Values and Rejection Regions (one sample t test): Should you Reject or Fail to Reject the Null Hypothesis?

In the fourth video in Statistics 101 Hypothesis Testing series, we will learn about critical values and rejection regions, and how they are used to decide if you should reject or fail to reject a null hypothesis.

In this set of statistics tutorials (Statistics 101), you will learn the concept of a null and alternative hypothesis, how a test statistic can be used to measure the compatibility of our data with the null hypothesis, the use of a significance level and p-values or critical regions, conclusions that we can make as well as the errors that may be made when drawing our conclusions.

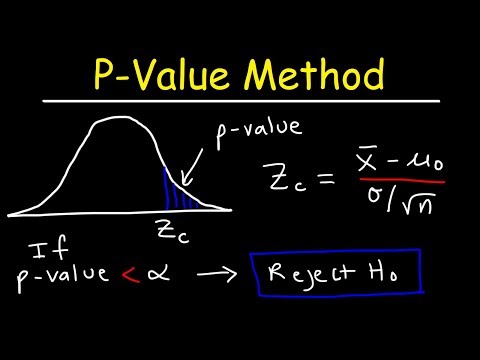
►A Critical Value or a Rejection Region can be applied to a test statistic to help us decide whether or not we believe the Null or Alternative hypothesis to be true. The larger the test statistic (in absolute value) the more evidence we have that the null is false and the alternative is true. But how large does the test statistic have to be before we believe the null to be false and the alternative to be true? The Critical Value can help us decide “how large is large enough for us to discredit the null and believe the alternative”?

►The One Sample t Test helps us decide whether or not we believe the sample mean is statistically different from a known or hypothesized population mean. The One Sample t Test is a parametric test. This test is also known as: Single Sample t Test or Student’s t test or when one assumes the population standard deviation is known, it is called the Z test. The test works by calculating a test statistic that measures how compatible the sample statistic (the sample mean in this case) is with the value that would be expected for the sample statistic if the null hypothesis were in fact true (the null hypothesized value). A p value is then calculated. The p value tells us the probability of obtaining a sample statistic as far, or further, from the null hypothesized value, if the null hypothesis were in fact true. The p value helps us decide whether or not we will believe the null hypothesis to be true or not.

►► Watch More:

Follow MarinStatsLectures

Our Team:
Content Creator: Mike Marin (B.Sc., MSc.) Senior Instructor at UBC.
Producer and Creative Manager: Ladan Hamadani (B.Sc., BA., MPH)

These videos are created by #marinstatslectures to support some courses at The University of British Columbia (UBC) (#IntroductoryStatistics and #RVideoTutorials for Health Science Research), although we make all videos available to the everyone everywhere for free.

Thanks for watching! Have fun and remember that statistics is almost as beautiful as a unicorn!

[aliabatool]

For those who are looking how we obtain -1.65 and -1.65 is obtained from t table( 5% p and n is unknown ) means look at z value for 0.05 ( negative becz 5%below 130). And for 121.75 value use formula : raw score=mean+(critical value* standard deviation) ....it becomes 130+(-1.65*5) =121.75 HOPE This HELPS

[ncg]

Thanks man! 4 years later, helped me a ton. <3

[alaksmcgregor]

These are incredibly helpful and well put together. Subscribed.

[krzysztofs]

Great video session. I rush to the last video session about H_{0}

[param]

What happens to the rejection region if the level of significance is changed from 0.05 to 0.10