filmov
tv
The Fourier Transform - Partial Differential Equations | Lecture 34

Показать описание
In the previous lecture we solved the heat equation on an infinite line to see that the solution is written as an integral over all wave numbers. In this lecture we investigate this integral operator, termed the Fourier transform. We derive the Fourier transform as the limit of a Fourier series as the domain becomes unbounded. As an example we show that Gaussians in physical space are transformed to Gaussians in Fourier/frequency space, and vice-versa. This property will be used in the next lecture when identifying the fundamental solution of the heat equation.
Follow @jbramburger7 on Twitter for updates.
Follow @jbramburger7 on Twitter for updates.
Fourier Transforms in Partial Differential Equations
The Fourier Transform - Partial Differential Equations | Lecture 34
Fourier Transform Technique for Solving PDEs (Part 1)
Solving the Heat Equation with the Fourier Transform
Properties of the Fourier Transform - Partial Differential Equations | Lecture 36
Lecture 42: Fourier Transforms and Partial Differential Equations
Solving the heat equation | DE3
Application of fourier transform to partial differential equations (Maths)
#78 B.Tech 2nd Year Engg. Mathematics-III Numerical Techniques // AKTU CLASSES By JEC | Ashish Sir
Solution of Partial Differential Equations using Fourier Transform - II
How to apply Fourier transforms to solve differential equations
How to Compute a FOURIER SERIES // Formulas & Full Example
Fourier Transform and the Heat Equation - Partial Differential Equations | Lecture 35
Fourier Transformation | Partial Differential equations | MSc Mathematics
ME565 Lecture 19: Fourier Transform to Solve PDEs: 1D Heat Equation on Infinite Domain
Solving differential equations with the Fourier transform
Solution of Partial Differential Equations using Fourier Transform - I
Multiple Fourier Transforms
(DE25) Fourier Transform Fundamentals
Fourier Analysis: Overview
How to compute a Fourier series: an example
Graphs that Reveal Hidden Frequencie , Fourier Transform & Series #maths
Fourier and Partial Differential Equations
Fourier Series introduction
Комментарии
 0:14:11
0:14:11
 0:22:51
0:22:51
 0:05:28
0:05:28
 0:11:28
0:11:28
 0:24:34
0:24:34
 0:18:44
0:18:44
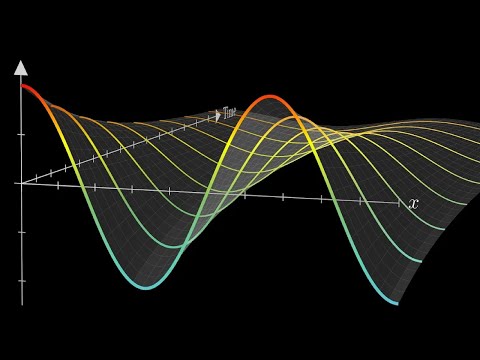 0:14:13
0:14:13
 0:28:55
0:28:55
 0:55:00
0:55:00
 0:33:22
0:33:22
 0:22:26
0:22:26
 0:13:16
0:13:16
 0:27:12
0:27:12
 0:23:37
0:23:37
 0:42:33
0:42:33
 0:31:07
0:31:07
 0:35:20
0:35:20
 0:08:42
0:08:42
 0:35:04
0:35:04
 0:07:29
0:07:29
 0:08:25
0:08:25
 0:00:13
0:00:13
 0:11:06
0:11:06
 0:05:12
0:05:12