filmov
tv
Intermediate Value Theorem Proof | Maths |Mad Teacher

Показать описание
This video explains the proof of Bolzano's Intermediate Value Theorem in the most simple and easy way possible. The statement of the proof is explained using the figure description as well.
Statement:
Let, “𝐼” be an interval and let, 𝑓:𝐼→ℝ be continuous on 𝐼. If 𝑎,𝑏∈𝐼 and if 𝑘∈ℝ satisfies 𝑓(𝑎) less than 𝑘 less than 𝑓(𝑏), then there exists a point 𝑐∈𝐼 between "𝑎" and "𝑏" such that 𝑓(𝑐)=𝑘.
Statement with figure description: 1:22
Proof: 2:22
Continuity of function (epsilon-delta definition):
--------------------------------GIVEAWAY RULES-----------------------------------------------
To win "Oxford Concise Dictionary of Mathematics" follow the instructions given below:
1) Subscribe to my channel
2) Like any of the video on this channel
3) Comment (on any of the video on this channel) which topic of Maths you want me to cover?
** Make sure your subscriptions are visible to public.
***Open Internationally.
****There will be two winners.
*****Winners will be announced when this channel hit 1000 SUBS.
GOOD LUCK!!
Leave your REQUESTS down below!
Please Share & SUBSCRIBE xoxo!
Statement:
Let, “𝐼” be an interval and let, 𝑓:𝐼→ℝ be continuous on 𝐼. If 𝑎,𝑏∈𝐼 and if 𝑘∈ℝ satisfies 𝑓(𝑎) less than 𝑘 less than 𝑓(𝑏), then there exists a point 𝑐∈𝐼 between "𝑎" and "𝑏" such that 𝑓(𝑐)=𝑘.
Statement with figure description: 1:22
Proof: 2:22
Continuity of function (epsilon-delta definition):
--------------------------------GIVEAWAY RULES-----------------------------------------------
To win "Oxford Concise Dictionary of Mathematics" follow the instructions given below:
1) Subscribe to my channel
2) Like any of the video on this channel
3) Comment (on any of the video on this channel) which topic of Maths you want me to cover?
** Make sure your subscriptions are visible to public.
***Open Internationally.
****There will be two winners.
*****Winners will be announced when this channel hit 1000 SUBS.
GOOD LUCK!!
Leave your REQUESTS down below!
Please Share & SUBSCRIBE xoxo!
A Proof of the Intermediate Value Theorem
A Basic Proof Using the Intermediate Value Theorem
Can you prove it? The Intermediate Value Theorem
Advanced Calculus 3.3 Intermediate Value Theorem proof
Intermediate Value Theorem Proof and Application, Bolzano's theorem
Intermediate Value Theorem and Finding Zeros | Calculus 1
Intermediate value theorem | Existence theorems | AP Calculus AB | Khan Academy
The Intermediate Value Theorem
Intermediate Value Theorem - Prove that Equation has a solution - A little Challenging Question
Proof of existence by I.V.T.
Proof of the Intermediate Value Theorem (ILIEKMATHPHYSICS)
Intermediate Value Theorem
Proving the Intermediate Value Theorem
Proofs Using the Intermediate Value Theorem
SIMPLE way to understand the Intermediate Value Theorem (IVT) in Calculus!
Intermediate Value Theorem || Proof || Real Analysis
Intermediate value theorem to prove a root in an interval (KristaKingMath)
How to Prove an Equation Has a Real Solution using the Intermediate Value Theorem
Intermediate Value Theorem Proof | Maths |Mad Teacher
Intermediate Value Theorem and Examples
Lecture 16: The Min/Max Theorem and Bolzano's Intermediate Value Theorem
Can Mathematicians Code? The Intermediate Value Theorem
Intermediate Value Theorem + Example on Proving a Root Exists
(1) Proofs From Conditions Of Intermediate Value Theorem
Комментарии
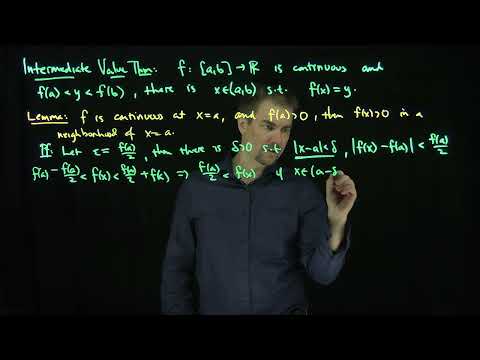 0:07:12
0:07:12
 0:08:03
0:08:03
 0:15:41
0:15:41
 0:08:46
0:08:46
 0:10:13
0:10:13
 0:08:26
0:08:26
 0:08:04
0:08:04
 0:08:40
0:08:40
 0:08:55
0:08:55
 0:10:07
0:10:07
 0:30:15
0:30:15
 0:11:04
0:11:04
 0:08:09
0:08:09
 0:05:03
0:05:03
 0:01:00
0:01:00
 0:14:59
0:14:59
 0:04:54
0:04:54
 0:07:11
0:07:11
 0:08:00
0:08:00
 0:06:34
0:06:34
 1:08:24
1:08:24
 0:11:31
0:11:31
 0:06:42
0:06:42
 0:08:14
0:08:14