filmov
tv
Differential Equations | Matrix Exponential Example: Diagonalizable Case

Показать описание
We present the general form for the matrix exponential of a diagonalizable matrix and a corresponding example.
Solving system of differential equations by matrix exponential
6.4 Exponential Matrix Example 1, Differential Equations
The Matrix Exponential
Differential Equations | The Matrix Exponential e^{tA}.
6.4 Exponential of a Matrix, Differential Equations
Matrix Exponential: How to calculate? (Step-by-step)
How (and why) to raise e to the power of a matrix | DE6
The Matrix Exponential
Advancing Calculus Research and Teaching with Wolfram Language
Differential Equations: matrix exponential and magic formula, 6-21-17, part 1
Differential Equations Lecture 26: Matrix Exponential
Solutions of systems of linear differential equations in terms of matrix exponentials
Matrix Exponentials
Differential Eqns. F22-21 -- Fundamental matrix and matrix exponentials
Differential Equations | Matrix Exponential Example: Diagonalizable Case
Differential Equations: The Exponential of a Matrix
e to a matrix
New Version Availalbe (3.8.101) Determine a Matrix Exponential and General Solution to x'=Ax
Linear Algebra: March 30, differential equations via the matrix exponential
Differential Equations: matrix exponential solutions, nonhomog. case, 10-24-17, part 2
Differential Equations: matrix exponential solutions, nonhomog. case, 10-24-17, part 1
Differential Equations | Matrix Exponential: 2x2 non-diagonalizable case.
Differential Equations: complex eigenvectors, matrix exponential, 10-19-17, part 2
Solving Systems of Differential Equations with Eigenvalues and Eigenvectors
Комментарии
 0:19:18
0:19:18
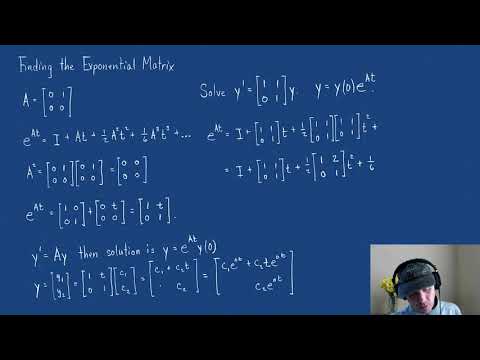 0:10:39
0:10:39
 0:15:32
0:15:32
 0:14:17
0:14:17
 0:14:52
0:14:52
 0:16:38
0:16:38
 0:27:07
0:27:07
 0:07:08
0:07:08
 1:24:32
1:24:32
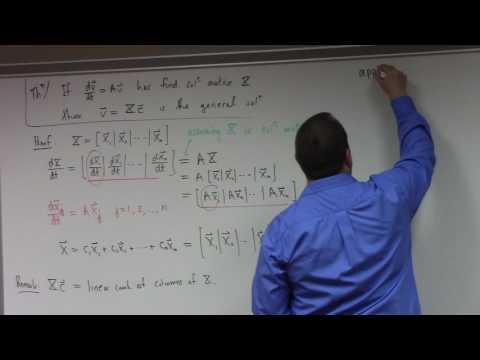 0:59:13
0:59:13
 0:53:50
0:53:50
 0:17:04
0:17:04
 0:08:18
0:08:18
 0:44:31
0:44:31
 0:10:04
0:10:04
 0:57:51
0:57:51
 0:12:30
0:12:30
 0:05:07
0:05:07
 0:52:40
0:52:40
 0:14:57
0:14:57
 0:59:51
0:59:51
 0:09:18
0:09:18
 0:13:44
0:13:44
 0:21:51
0:21:51