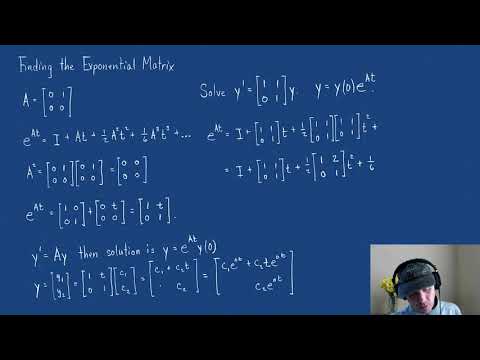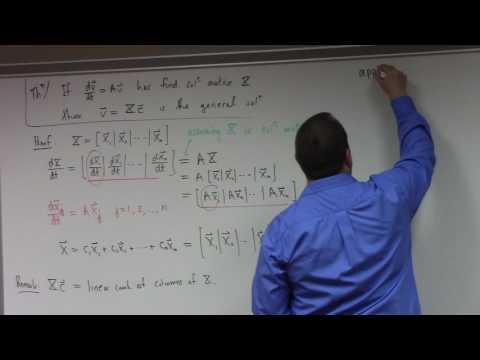Differential Equations | Matrix Exponential: 2x2 non-diagonalizable case.

Показать описание

We present a general strategy for finding the matrix exponential of a 2x2 matrix that is not diagonalizable. An example is included.

Рекомендации по теме

Комментарии

This video deserves a revamp; it's a nice and interesting topic and your set for the video was already clear and catching but your exposition technique improved so much that this video aged quite bad if compared to those new

LucaIlarioCarbonini

Agreed! Very nice video on a subject worth diving into: Jordan canonical matrices.
This being said, I was a bit puzzled by the summation of n*lambda^(n-1), because the sum starts at 0 and (-1)! Is not good.
One workaround would be to write it as sum( d/dlambda( lambda^(n)))= d/dlambda(sum of lambda^n)= d/dlambda(exp(lambda)) = exp(lambda)

benjaminbrat

02:55 There should be not
P^(-1) * (...) * P
but
P * (...) * P^(-1)

damianbla

Great work but I believe the final matrix is [[e3, 0], [-2e3, 0]]

mekbebtamrat

Differential Equations | Matrix Exponential: 2x2 non-diagonalizable case.

Solving system of differential equations by matrix exponential

6.4 Exponential Matrix Example 1, Differential Equations

The Matrix Exponential

Differential Equations | The Matrix Exponential e^{tA}.

6.4 Exponential of a Matrix, Differential Equations

Matrix Exponential: How to calculate? (Step-by-step)

How (and why) to raise e to the power of a matrix | DE6

The Matrix Exponential

Differential Equations: matrix exponential and magic formula, 6-21-17, part 1

Differential Equations Lecture 26: Matrix Exponential

Solutions of systems of linear differential equations in terms of matrix exponentials

Matrix Exponentials

Differential Eqns. F22-21 -- Fundamental matrix and matrix exponentials

Differential Equations | Matrix Exponential Example: Diagonalizable Case

Differential Equations: The Exponential of a Matrix

New Version Availalbe (3.8.101) Determine a Matrix Exponential and General Solution to x'=Ax

e to a matrix

Linear Algebra: March 30, differential equations via the matrix exponential

Differential Equations: matrix exponential solutions, nonhomog. case, 10-24-17, part 2

Differential Equations | Matrix Exponential: 2x2 non-diagonalizable case.

Differential Equations: matrix exponential solutions, nonhomog. case, 10-24-17, part 1

Differential Equations: complex eigenvectors, matrix exponential, 10-19-17, part 2

Differential Equations: matrix exponential, 6-20-17, part 3

Solving Systems of Differential Equations with Eigenvalues and Eigenvectors