filmov
tv
How to find the component form and magnitude of a vector
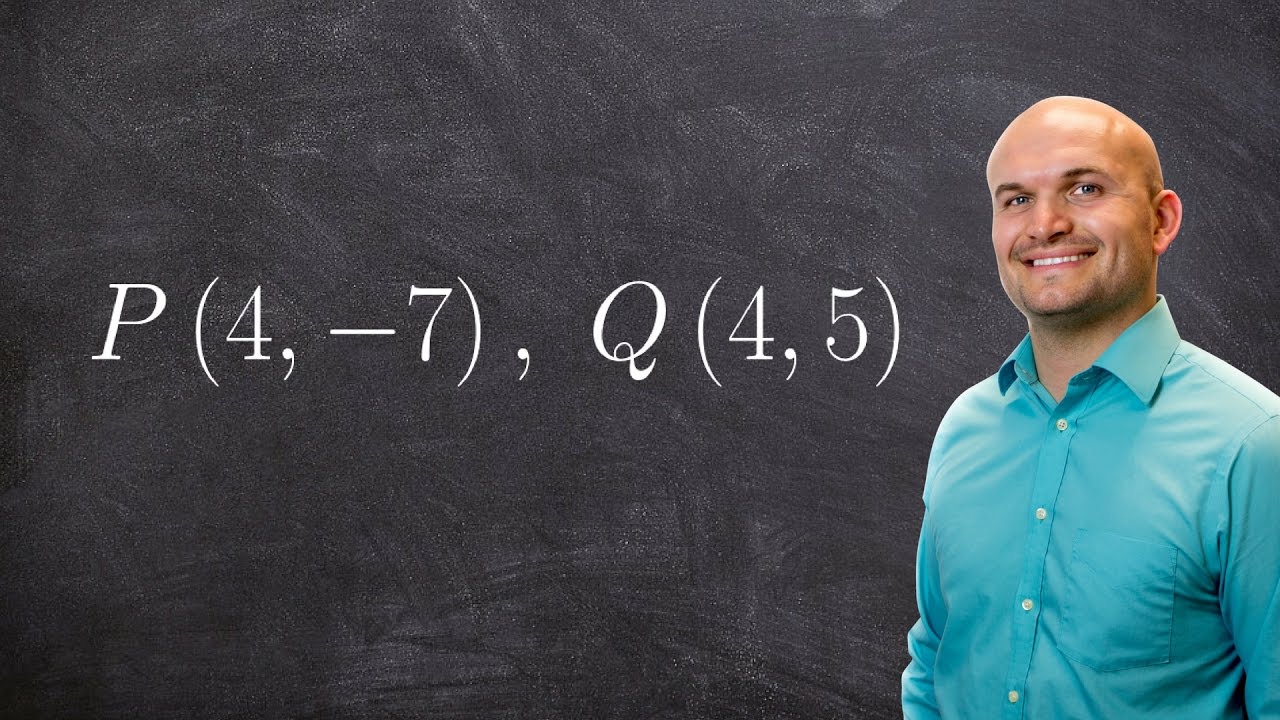
Показать описание
Learn how to write a vector in component form given two points and also how to determine the magnitude of a vector given in component form. Given two point vectors with one representing the initial point and the other representing the terminal point. The component form of the vector formed by the two point vectors is given by the components of the terminal point minus the corresponding components of the initial point. i.e. given the initial point as P(p1, p2) and the terminal point as Q(q1, q2), the component form of the vector formed by the two vectors is given by V(q1-p1, q2-p2).
The magnitude of a vector given in component form is given by the square root of the sum of the squares of each component of the vector. i.e given a vector V(p, q), the magnitude of the vector is given by |V| = sqrt(p^2 + q^2).
#trigonometry#vectors
#vectors
The magnitude of a vector given in component form is given by the square root of the sum of the squares of each component of the vector. i.e given a vector V(p, q), the magnitude of the vector is given by |V| = sqrt(p^2 + q^2).
#trigonometry#vectors
#vectors
How To Find The Components of a Vector Given Magnitude and Direction
How to find the component form of a vector
How to find the component form and magnitude of a vector
How to Find the Component Form of a Vector
17 - Calculating Vector Components in Physics, Part 1 (Component form of a Vector)
How to find the component at Altium PCB File
How to find the component form of a vector given the magnitude and direction
Vectors Component Form
Discover the Components of the UiPath Platform [Automation Business Analyst Series]
Learn how to find the component form and magnitude of a vector
Finding the component form and magnitude of a vector
How to find the Component form and magnitude of a Vector (Vectors Lesson 4)
HOW TO FIND YOUR VST,VST3, and COMPONENT FOLDERS ON MAC
Writing a vector in component form given a magnitude and direction
How to find the component and magnitude of a vector
What is a Component of a Graph? | Connected Components, Graph Theory
Where to find Azrael drone component #CX2067 - Tom Clancy’s Ghost Recon Breakpoint
Find the Component Form of a Vector by Analyzing a Graph (2D)
component of a vector along another vector
CRP-5 *HOW TO * Find Crosswind Component [ Given wind velocity and runway ]
SMD Resistor package codes and Footprint. SMT component Sizes. SMD Resistor Coding Explained.
Learn to Fly - Calculating Crosswind Component
Magnitude and direction of vectors using component method
Ex: Find the Component Form of a Vector in Space Given the Initial and Terminal Point
Комментарии
 0:08:40
0:08:40
 0:05:04
0:05:04
 0:05:31
0:05:31
 0:05:50
0:05:50
 0:29:41
0:29:41
 0:00:43
0:00:43
 0:02:08
0:02:08
 0:02:29
0:02:29
 1:10:01
1:10:01
 0:05:16
0:05:16
 0:05:16
0:05:16
 0:09:49
0:09:49
 0:00:21
0:00:21
 0:03:38
0:03:38
 0:05:16
0:05:16
 0:05:17
0:05:17
 0:01:05
0:01:05
 0:03:41
0:03:41
 0:04:17
0:04:17
 0:01:25
0:01:25
 0:04:42
0:04:42
 0:01:31
0:01:31
 0:14:57
0:14:57
 0:02:42
0:02:42