filmov
tv
How to find many vectors orthogonal to given in vector three space

Показать описание
Coplanar vectors problems can be solved using two different strategies as shown in the video. Consider linear combination of scalar triple product of vectors.
#MCV4U_Vectors #linearlydependent #linearcombination #scalartripleproduct #coplanar #coplanarvectors #globalmathinstitute #vectorprojection #scalarprojection #vectors_MCV4U #Vectors_IB #GCSEvector
#MCV4U_Vectors #linearlydependent #linearcombination #scalartripleproduct #coplanar #coplanarvectors #globalmathinstitute #vectorprojection #scalarprojection #vectors_MCV4U #Vectors_IB #GCSEvector
How to find many vectors orthogonal to given in vector three space
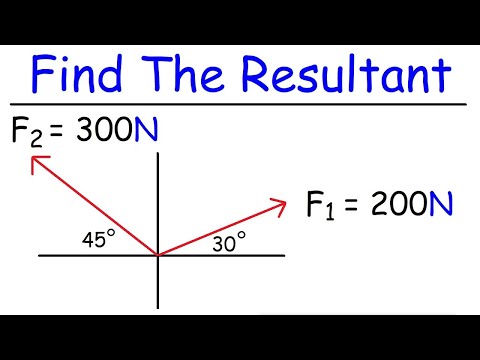
How To Find The Resultant of Two Vectors
Adding Vectors: How to Find the Resultant of Three or More Vectors
How to Find a Unit Vector Perpendicular to Another Vector 8i + 4j - 6k
Everything You Need to Know About VECTORS
Find Unit Vector and Perpendicula Vector in R3
How To Find The Unit Vector
Addition of Vectors By Means of Components - Physics
How to determine if one vector is in the span of other vectors?
How to find a vector perpendicular to two vectors with Dot Product MCV4U Test
Position Vectors and Displacement Vectors - Physics
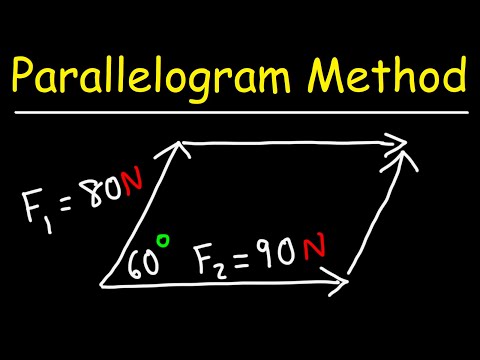
How To Use The Parallelogram Method To Find The Resultant Vector
How to find the vector with given magnitude and same direction of another vector
How to find the Angle between Vectors
Vector Databases simply explained! (Embeddings & Indexes)
Perpendicular Vectors in R2
How to add Vectors Using the Component Method
Linear Algebra Example Problems - Spanning Vectors #1
Find Perpendicular Vectors in R3 with Dot Product
Adding 3 or More Vectors Graphically (Add Vectors in Physics)
How to find the unit vector perpendicular to vector a and vector b best example
Linear Algebra - Lecture 7 - Linear Combinations and Vector Equations
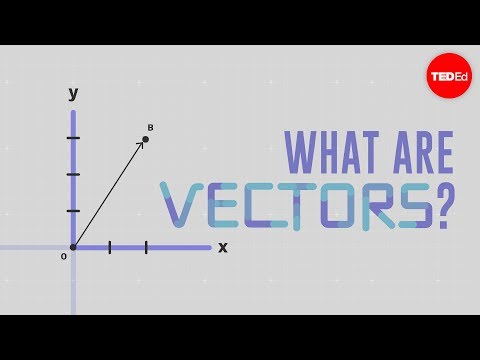
What is a vector? - David Huynh
The Vector Equation of Lines | Multivariable Calculus
Комментарии
 0:06:15
0:06:15
 0:11:10
0:11:10
 0:14:44
0:14:44
 0:10:42
0:10:42
 0:17:42
0:17:42
 0:05:21
0:05:21
 0:05:08
0:05:08
 0:15:21
0:15:21
 0:05:00
0:05:00
 0:07:22
0:07:22
 0:07:18
0:07:18
 0:05:11
0:05:11
 0:04:50
0:04:50
 0:05:44
0:05:44
 0:04:23
0:04:23
 0:05:26
0:05:26
 0:08:54
0:08:54
 0:04:31
0:04:31
 0:06:21
0:06:21
 0:13:24
0:13:24
 0:03:51
0:03:51
 0:08:10
0:08:10
 0:04:41
0:04:41
 0:05:30
0:05:30