filmov
tv
Time complexity analysis: asymptotic notations - big oh, theta ,omega

Показать описание
See complete series on time complexity here
In this lesson we will introduce you to the concept of asymptotic notations in time complexity analysis of an algorithm.
In this lesson we will introduce you to the concept of asymptotic notations in time complexity analysis of an algorithm.
Time complexity analysis: asymptotic notations - big oh, theta ,omega
Time Complexity of Algorithms and Asymptotic Notations [Animated Big Oh, Theta and Omega Notation]#1
Learn Big O notation in 6 minutes 📈
Big-O Notation in 100 Seconds
1.8.1 Asymptotic Notations Big Oh - Omega - Theta #1
Big-O notation in 5 minutes
Asymptotic Notations 101: Big O, Big Omega, & Theta (Asymptotic Analysis Bootcamp)
Big-O Notation - For Coding Interviews
Asymptotic Analysis (Solved Problem 1)
Big O Notation, Time Complexity | DSA
Time complexity | Big O Notation
Guidelines for Asymptotic Analysis (Part 1)
L-1.3: Asymptotic Notations | Big O | Big Omega | Theta Notations | Most Imp Topic Of Algorithm
Big O Notation - Full Course
Introduction to Big O Notation and Time Complexity (Data Structures & Algorithms #7)
What Is Algorithm Complexity? #shorts
Time complexity analysis: Asymptotic Notations - Big oh, Theta ,Omega - Coding With Mr. Ash
Big O notation - Data Structures & Algorithms Tutorial #2 | Measuring time complexity
Basics of Asymptotic Analysis (Part 1)
What Is Asymptotic Analysis? And Why Does It Matter? A Deeper Understanding of Asymptotic Notation.
Big Oh(O) vs Big Omega(Ω) vs Big Theta(θ) notations | Asymptotic Analysis of Algorithms with Example...
Time Complexity and Big O Notation - Data Structures and Algorithms
Calculating Time Complexity | Data Structures and Algorithms| GeeksforGeeks
Time complexity explained #mysirg
Комментарии
 0:10:40
0:10:40
 0:11:21
0:11:21
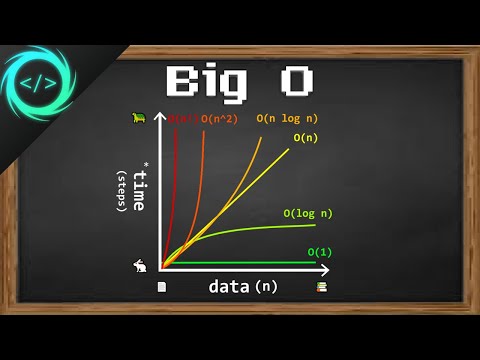 0:06:25
0:06:25
 0:01:40
0:01:40
 0:15:46
0:15:46
 0:05:13
0:05:13
 0:23:16
0:23:16
 0:20:38
0:20:38
 0:07:23
0:07:23
 0:21:17
0:21:17
 0:00:58
0:00:58
 0:05:04
0:05:04
 0:14:25
0:14:25
 1:56:16
1:56:16
 0:36:22
0:36:22
 0:00:25
0:00:25
 0:10:40
0:10:40
 0:12:31
0:12:31
 0:06:32
0:06:32
 0:08:05
0:08:05
 0:28:50
0:28:50
 0:14:56
0:14:56
 0:08:05
0:08:05
 0:01:01
0:01:01