filmov
tv
Polynomials Class 10

Показать описание
Polynomials : Important Questions and Formulas on Polynomials for Class 10 are discussed! Your concepts on Polynomials will become super clear!
Special Offer on our Full Courses!
At Manocha Academy, learning Science and Math is Easy! The school coursework is explained with simple examples that you experience every day! Yes, Science & Math is all around you! Let's learn every day from everyday life!
Special Offer on our Full Courses!
At Manocha Academy, learning Science and Math is Easy! The school coursework is explained with simple examples that you experience every day! Yes, Science & Math is all around you! Let's learn every day from everyday life!
Polynomials Class 10
Class 10 CBSE Maths - Polynomials In 20 Minutes | Xylem Class 10 CBSE
Class 10 CBSE Maths | Chapter 2 - Polynomials / Part - 1| Xylem Class 10 CBSE
Class 10 CBSE Maths | Polynomials | Full Chapter Revision | Xylem Class 10 CBSE
Complete Polynomials Class 10 in 20 Mins | CBSE Class 10 Maths | Polynomial One Shot Revision
Polynomials gr10 part 1
Polynomials Class 10 | Maths | Asaltu | Shimon Sir | Vedantu Master Tamil |
CBSE Class 10 Maths | Polynomials | Chapter 2 | Full Chapter | Exam Winner
Polynomials FULL CHAPTER | Class 10th Mathematics | Chapter 2 | Udaan
Solving Polynomial Equations - Grade 10 Math
Class 10th Polynomials Maths One Shot #cbse2024 Shimon Sir | V Master Tamil |
Polynomials Class 10 Term 1 | One Shot Lecture | Full NCERT Covered
Class 10 CBSE Maths - Chapter 2 | Polynomials - Full Chapter Revision | Xylem 10 CBSE
Class 10 Maths | Chapter 2 | Introduction Part 1 | Polynomials | NCERT
Polynomials Marathon | Part 1 | Class 10 Maths | CBSE 2025 |🔥 Shimon Sir
Class 10 CBSE Maths - Polynomials | Concept Revision | Xylem Class 10 CBSE
How to Divide Polynomials using Long Division - Polynomials
Polynomials| Part-1| Class 10|Introduction,Exercise-9.1|Mathematics| NCERT / CBSE
Class 10 Maths Chapter 2 Polynomials Concept in 10 Minutes | CBSE 10 Maths 2025
Chapter 2 Polynomials Introduction part 1 CBSE maths class 10 in Malayalam
Polynomials Most Expected Questions | Class 10 | CBSE 2025🔥 Shimon Sir
Polynomials | Class 10 Maths AP/TS | Chapter – 3 | Part – 1 | All Concepts | Ramesh Sir Maths
Polynomials Marathon Problem Solving | Class 10 | CBSE 2024 |🔥 Shimon Sir
Polynomials Complete Chapter In 13 Minutes | Class 10th Board
Комментарии
 0:23:33
0:23:33
 0:22:45
0:22:45
 1:13:50
1:13:50
 2:06:45
2:06:45
 0:25:26
0:25:26
 0:10:23
0:10:23
 0:54:47
0:54:47
 1:11:27
1:11:27
 4:04:48
4:04:48
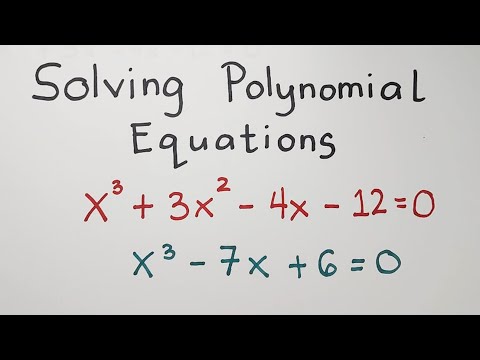 0:12:02
0:12:02
 2:03:07
2:03:07
 0:54:55
0:54:55
 1:10:26
1:10:26
 0:10:06
0:10:06
 0:51:08
0:51:08
 0:32:44
0:32:44
 0:11:44
0:11:44
 0:51:48
0:51:48
 0:10:11
0:10:11
 0:28:28
0:28:28
 1:24:43
1:24:43
 1:01:58
1:01:58
 1:03:02
1:03:02
 0:13:37
0:13:37