Integral Test for Series: Why It Works

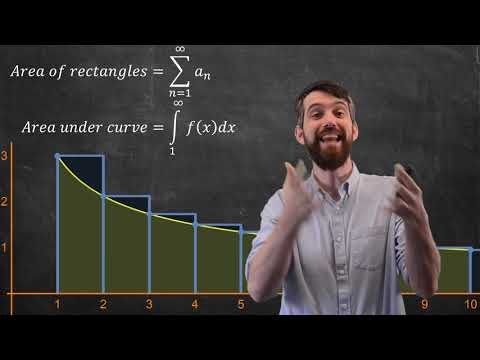
In this video, I give a little geometric argument about the integral test for series and why it works when we compare our series to an improper integral.

[thecrankyangel]

You have no idea how "right on time" this video is. My whole class loves you!

[MorvyJ]

correction: monotone functions*. simply bounded or everywhere defined isn't enough. take for example the series: 1/n^2 + (sin(n*pi))^2. At every natural number n, (sin(n*pi))^2 = 0, so the series converges., however the integral clearly diverges since (sin(n*pi))^2 does not approach zero as a limit.

[Diegownz]

this was super helpful! finally someone who explained why you use the left or right version of the sum representation

[Paleopalescence]

Patric JMT does it again! Your videos are so brilliant, so nail-biting I think I may be developing a nonfunctional habit from watching your videos, with all the nail-biting. I may be developing TMJ! Now I can go around telling people I got TMJ from watching Patric JMT. They won't know what I'm talking abut but that's okay, I'm used to that.

[alcesmir]

It's not about the sound quality. It's the popping that occurs when pronouncing letters like p (caused by strong bursts of air). A pop filter (basically a small sheet of some fabric I can't remember) helps stopping these bursts and thus eliminates most of the pops.

[patrickjmt]

never heard of that, i will check it out

[VictorDo]

IF only you posted this a few weeks into the semester and I would have been golden!

[toofresh]

@ freelapdane. 1/x is the harmonic series and its exponent is equal to one. 1/x^2 is a p-series, in which the exponent is greater than one, so it will converge.

[christymoen]

Quick question for you Patrick. How do you film your film? Is there a webcam over your shoulder? I only ask as i have a coursework where you have to make a video of you explaining a concept, and I really like your style! Thanks man!

[SyedFaraz]

awesome timing, i was just preparing for seq and ser. you should have separate playlist for it. thanks

[MorvyJ]

I wonder about what restrictions there are for when you are allowed to use this test. The series 1/(n-0.5)^2 will converge [by limit comparison test], but the integral will diverge since as x approaches 0.5, it shoots off towards infinity, p test: p=2. Clearly it should be true for monotone decreasing sequences, and by symmetry for monotone increasing sequences., but it should be occasionally true for more complicated non-monotone sequences. Perhaps if the function must be bounded

[Pooua]

If he would simply position the mic so he isn't spitting into it, it would help. Usually, the mic is supposed to be positioned to the side of the mouth (depends on the mic).

[KennyNumberOne]

its awesome that he posted this today because i'm doing the same topic, preventing me from procrastinating lol

[justinlui]

Quick question, I will be taking Elementary Linear Algebra next semester and I hear it's even more abstract and difficult than Calc 2. Have you covered topics pertaining this subject in your vast collection? I'm not sure where your brilliance has ended :)

[DoggoWillink]

I'm so pissed at math right now. Well, more at myself I guess. I took an exam yesterday and got a problem wrong (I realized after walking out the door) because of a really subtle interpretation error. I knew literally EVERYTHING too. That's friggin' math for you.

[sara]

Patrick would you download a video about the difference between balanced and unbalanced coin cause I can't know the difference between them?

[amak]

You are in for serious fun, man. These things can become a real pain real quick.

[patrickjmt]

i position it off to the side. i am not eating it while i make the video...

[Dtho]

so it's pretty similar to direct comparison of series?

[DoggoWillink]

If they gave you more time for these long, arithmetic-ridden exams, it would be a little more fair. I'm so OCD with math, it takes
me forever to do things because I recheck everything, even when I know I'm right.