filmov
tv
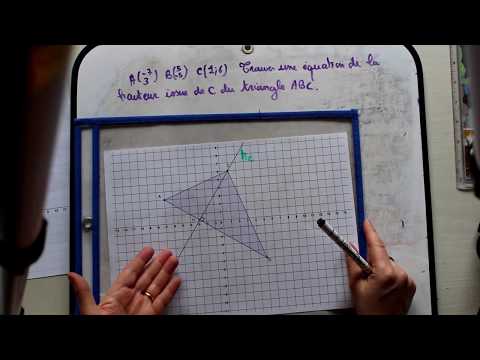
Équation de la HAUTEUR d'un Triangle - Exercice Corrigé - Première

Показать описание
#maths #première #exercicecorrigé Comment trouver l'équation cartésienne de la hauteur d'un triangle ?
La hauteur d’un triangle est une droite qui passe par un sommet et qui est perpendiculaire au côté opposé.
Pour établir une équation de droite, il nous faut :
• un vecteur (directeur ou normal) et
• un point de passage.
Coordonnées du vecteur (AB) ⃗ avec deux points A(x_A;y_A ) et B(x_B;y_B ) :
(AB) ⃗((x_B-x_A)¦(y_B-y_A ))
Une équation cartésienne de la forme : ax+by+c = 0
On a vu qu’elle a comme vecteur directeur possible : u ⃗((-b ; a)
(direction parallèle à la droite)
Elle a aussi comme vecteur normal possible : n ⃗(a ; b)
(direction perpendiculaire à la droite)
Pour trouver la dernière inconnue « c » il nous faut un point de passage :
Si le point A(x_A;y_A ) appartient à la droite, on peut écrire :
ax_A+by_A+c=0
En isolant « c » on obtient sa valeur numérique.
Équation de la HAUTEUR d'un Triangle - Exercice Corrigé - Première
Déterminer une équation cartésienne d'une hauteur d'un triangle - Première Spécialité...
Equations cartésiennes et produit scalaire - Exercice devoir - Hauteur dans un triangle
EXERCICE: Déterminer une équation d'une hauteur dans un triangle - 3eme année du Collège
Équation de la MÉDIATRICE d'un Segment - Exercice Corrigé - Première
Déterminer une équation de cercle (1) - Première
1ère S - Produit Scalaire : déterminer l'équation d'une hauteur dans un triangle
Équation cartésienne d'une hauteur, d'une médiatrice.
Équation de la MÉDIANE d'un Triangle - Exercice Corrigé - Première
Equation d une hauteur de triangle
Comment tracer les 3 hauteurs d’un triangle #maths #mathscollege #shorts
Déterminer une équation cartésienne d'une droite (1) - Seconde
Construire une médiatrice ou une hauteur - Cinquième
Déterminer une équation cartésienne d'une droite (vecteur normal) - Première
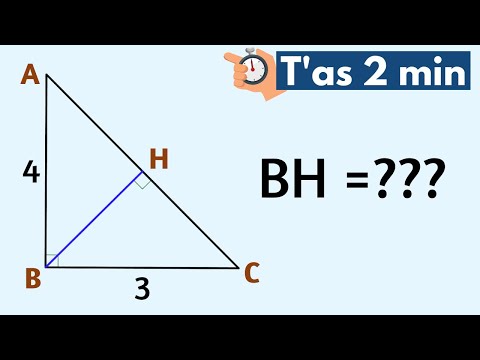
T'as 2 minutes ! Calculer une longueur
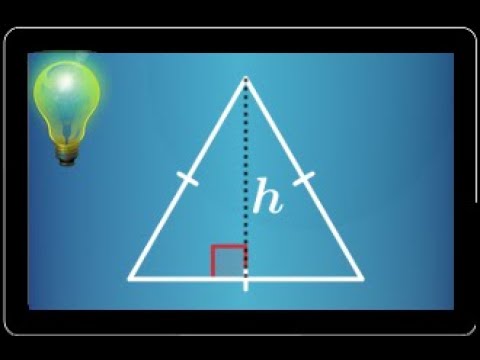
hauteur d'un triangle équilatéral • Démontrer la formule h=√3/2a • Exercice classique • Seconde...
Partager. équation réduite de la hauteur d'un triangle
🔴MATHSCLIC EXERCICE | ÉQUATION CARTÉSIENNE D'UNE DROITE DÉFINIE PAR UN POINT ET UN VECTEUR NORM...
LE COURS - Équations de droites - Seconde
Formules de calcul d'aire de quelques formes géométriques.
hauteur d'un triangle
Formules : Vitesse, Distance et Temps#maths #mathscollege #shorts
Faire 2 carrés avec 3 allumettes !
suite de l exo 18 equation de hauteur determination des coordonnées d un orthocentre
Комментарии
 0:05:28
0:05:28
 0:02:53
0:02:53
 0:11:59
0:11:59
 0:08:42
0:08:42
 0:05:42
0:05:42
 0:03:47
0:03:47
 0:09:48
0:09:48
 0:06:07
0:06:07
 0:05:31
0:05:31
 0:07:27
0:07:27
 0:00:17
0:00:17
 0:03:19
0:03:19
 0:04:39
0:04:39
 0:03:47
0:03:47
 0:03:15
0:03:15
 0:07:00
0:07:00
 0:10:58
0:10:58
 0:03:36
0:03:36
 0:21:16
0:21:16
 0:00:39
0:00:39
 0:00:16
0:00:16
 0:00:19
0:00:19
 0:00:16
0:00:16
 0:15:05
0:15:05