filmov
tv
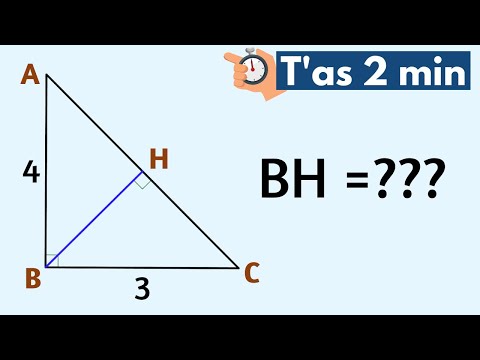
T'as 2 minutes ! Calculer une longueur

Показать описание
Déterminer une longueur rapidement : géométrie de collège utilisée pour vite trouver la bonne réponse !
T'as 2 minutes ! Calculer une longueur
Quel est le pourcentage de garçons? T'as 2 minutes !
T'as 2 minutes, trouve la 5ème note !
Calculer 500² - 505 x 495 -T'as 2 minutes !
1 minute pour calculer un pourcentage
2 MIN POUR... comprendre la gamme pythagoricienne !
CONVERTIR des unités de TEMPS (secondes, minutes, heures, jours, années) | Outils MATHÉMATIQUES
Calculer une vitesse moyenne puis une distance • conversion heure minute • Formule V=d/t • Quatrième...
Day 2: Part 1
Naël se rase les cheveux🧑🦲😯 |TIKTOK:➡️naelleziente
Calculs avec des heures et des durées
Calculate hours between two times
How to Calculate Faster than a Calculator - Mental Maths #2| Addition and Subtraction
ABACUS Level 2 | Addition & Subtraction Video | Saksham Abacus Academy #maths #school #kids #sho...
Tricky Test Problem - How To Solve In 2 Minutes
Apprendre le calcul du taux de variation en 2 minutes ! 🚀 [SES - 2nd]
Convertir 's' en 'h-min-s' - Sixième
Additionner des fractions ✅ exemples faciles | Maths
Calcul PM Medicament dosé à 10%
How To Calculate Faster than a Calculator
calculer la vitesse moyenne en m/min et km/h • conversion heure minute • Formule V=d/t • Quatrième...
Comprendre les fractions en 1 minute.
Calculer le Taux de Marge, Retrouver le Prix de Vente ou Prix d'Achat à partir du Taux de Marge...
R One x GTNN x Dj Maxx - Faut pas calculer (Run Hit)
Комментарии
 0:03:15
0:03:15
 0:03:47
0:03:47
 0:02:53
0:02:53
 0:02:17
0:02:17
 0:00:58
0:00:58
 0:02:09
0:02:09
 0:04:35
0:04:35
 0:06:50
0:06:50
 2:02:07
2:02:07
 0:00:15
0:00:15
 0:04:59
0:04:59
 0:00:45
0:00:45
 0:08:00
0:08:00
 0:00:23
0:00:23
 0:02:13
0:02:13
 0:03:04
0:03:04
 0:07:07
0:07:07
 0:03:54
0:03:54
 0:02:32
0:02:32
 0:00:30
0:00:30
 0:04:54
0:04:54
 0:00:49
0:00:49
 0:05:37
0:05:37
 0:03:20
0:03:20