filmov
tv
Superposition and the Wronskian - Ordinary Differential Equations | Lecture 13

Показать описание
In this lecture we introduce the basic existence and uniqueness theory for linear second order differential equations. We also present the principle of superposition, which then leads to the Wronskian. We show that with the Wronskian we can identify if two solutions form a fundamental solution set, thus giving us two solutions that can be used to satisfy any initial conditions.
This course is taught by Jason Bramburger for Concordia University.
Follow @jbramburger7 on Twitter for updates.
This course is taught by Jason Bramburger for Concordia University.
Follow @jbramburger7 on Twitter for updates.
Superposition and the Wronskian - Ordinary Differential Equations | Lecture 13
Linear Independence of Functions & The Wronskian
Differential Equations - 31 - The Wronskian
🔵19 - Fundamental Sets of Solution and Wronskian, Principle of Superposition of Differential Equ&apo...
The Wronskian for systems of differential equations
The Theory of 2nd Order ODEs // Existence & Uniqueness, Superposition, & Linear Independence
Second Order Linear ODEs Superposition of Solutions
ODE | Principle of superposition
Differential Equations - 4.1 Higher Order Linear ODEs (Lecture Part 2 of 2)
The Wronskian | Lecture 12 | Differential Equations for Engineers
Superposition Principle and Wronskian in Linear Algebra and Geometry
DEqns: L6, linear independence and the wronskian, part 1, 9-15-16
Lecture 10: The Wronskian
Section 3.2: Solutions of Linear Homogeneous Equations (Part 2, Superposition Principle, Wronskian)
Linear operators. Understanding the Wronskian
Linear Dependence and Linear Independence of Functions, Wronskian, Superposition Principle
Superposition Principle, Wronskian
superposition
Differential Equations: annihilator method, superposition, 6-15-17, part 2
Prerequisite Lecture 3: Second Order Linear Homogeneous Equations and the Wronskian
superposition principle,linear independent&dependent,Basis,Wronskian problems
The Wronskian Formula for a Particular Solution
Homogeneous Linear Differential Equations & Principle of Superposition
Math 261 - 3.2 - Solutions of Linear Homogeneous Equations; The Wronskian
Комментарии
 0:31:16
0:31:16
 0:09:59
0:09:59
 0:06:49
0:06:49
 0:26:33
0:26:33
 0:03:09
0:03:09
 0:11:19
0:11:19
 0:06:02
0:06:02
 0:04:18
0:04:18
 0:35:58
0:35:58
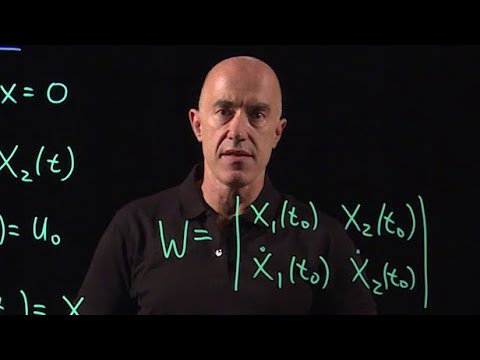 0:08:13
0:08:13
 0:05:37
0:05:37
 0:59:51
0:59:51
 0:46:13
0:46:13
 0:27:04
0:27:04
 1:03:05
1:03:05
 0:38:47
0:38:47
 0:20:31
0:20:31
 0:30:07
0:30:07
 0:59:51
0:59:51
 0:30:05
0:30:05
 0:21:58
0:21:58
 0:08:04
0:08:04
 0:04:16
0:04:16
 0:31:33
0:31:33