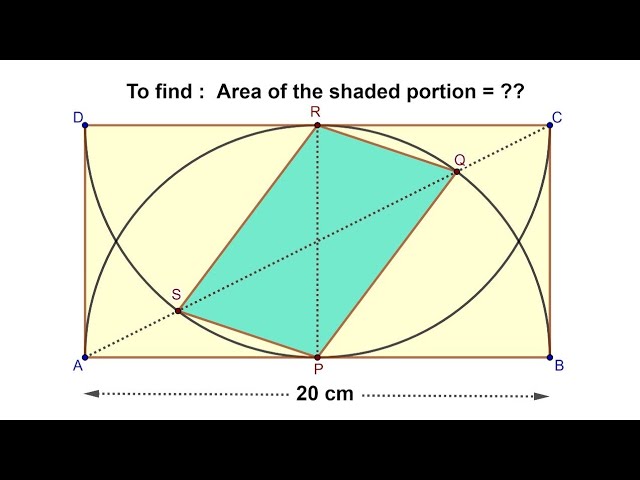
To find the shaded area. || ABCD is a rectangle with length AB = 20 cm. || Inscribed semicircles.

In this video discussion, we will learn how to find the shaded portion's area given in the diagram. ABCD is a rectangle having length AB = 20 cm. Two semicircles are inscribed according to the diagram. Find the yellow shaded quadrilateral's area.

#Tangent_Secant_Theorem
#Pythagoras_Theorem
#Triangles_having_Common_vertex

Useful for :

#NTSE, #GRE, #IITJEE, #IOQM, #RMO,
#INMO, #ISI, #CMI, #MAT, #CAT, #SAT, #BITSAT, #PET, #CET, #MCA, #NDA, #CDS, #SSC, #KVPY, #RRB

[ROCCOANDROXY]

In general, letting AB = a implies PQRS is a parallelogram and Area(PQRS) = 3 /20 * a^2.

[timc]

...or perhaps also: Let A be Origin, (0, 0), then S is pt of intersection of : y = (1/2)x and (y - 10)^2 + (x - 10)^2 = 10^2,
giving : (5/4) x^2 - 30x + 100 = 0, after subst. for y, or: x^2 - 24x + 80 = 0, so S is (4, 2), so altitude of triangle with base = 10 is
(10 - 4) = 6, so req'd area = 2*(1/2)* 6*10 = 60.

[davidseed]

coordinate geometry.
find the position of point Q..
origin at P
circle x²+y²≉100
diagonal y=5+x/2
intercept x²+(5+x/2)²≉100

x²+25+5x + (x/2)²≉100

5x/4²+5x≉75
multiply by 4/5

x²+4x-60=0
(x+10)(x-6)=0
x is positive so x=6
area of parallelogram is twice area of PQR
which has base 10 and vertical height (x=6)
Answer =2*10*6/2=60

[jimlocke]

Alternative solution method, probably not better or worse than Rakesh's, just another way of solving. At about 5:15, Rakesh has found that length OQ = 3√5. Examine ΔPOQ. Note that PQ is a radius of the semicircle through A, R and B, so PQ has length 10. OP has length 5. Drop a perpendicular from point O to line segment PQ. Label the intersection with PQ as point T. Let length OT = x and PT = y, therefore length TQ = 10 - y. We have 2 right triangles, ΔPTO and ΔQTO. Using Pythagorean theorem on ΔPTO, 5² = x² + y² or, expanded, 25 = x² + y². For ΔQTO, (3√5)² = x² + (10 - y)² or, expanded, -55 = x² - 20y + y². Subtract 25 = x² + y² to get -80 = - 20y, or y = 4. Substituting y = 4 in 25 = x² + y² and solving for x, we find x = 3. (The very familiar 3 - 4 - 5 right triangle!) If we extend line segment OT to RS and label the intersection U, we note that OU also has length 3 by symmetry, so TU has length 6. If PQ is the base of PQRS, then TU is its height. PQ has length 10 and TU length 6, area of PQRS is the product, or 60. Units are cm for all lengths, so area is 60 cm², just as Rakesh found.