WildLinAlg11: Applications of 3x3 matrices

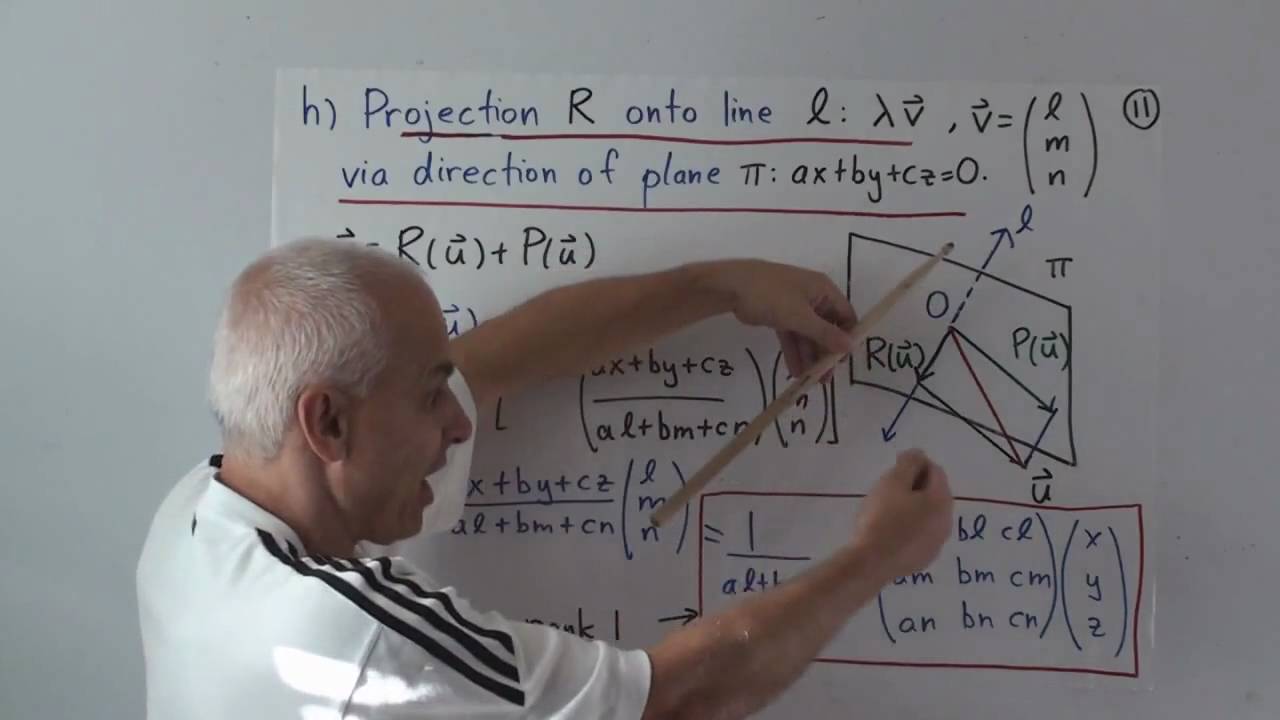
Three dimensional space has a rich variety of linear transformations, including dilations, reflections and rotations. These are reflected in the algebra of 3x3 matrices.

NJ Wildberger is also the developer of Rational Trigonometry: a new and better way of learning and using trigonometry---see his WildTrig YouTube series under user `njwildberger'. There you can also find his series on Algebraic Topology, History of Mathematics and Universal Hyperbolic Geometry.

[unswelearning]

Hi MrFunatabi I think you are right, and what I am describing here should actually be rotation by negative theta rather than theta!

[saadamehdi]

Hi. How do you transform a quotient column matrix with x y and z in each row, into a matrix into a product of an  x y z column matrix and a 3x3 matrix ? Where has it been said ealier in the serie ?
Thanks, mehdi

[eyupfirataydin]

Hi professor

Imagine a point in a given Cartesian space, X, Y, Z of this space are both transformed and rotated arbitrarily. How would my point can be expressed with respect to that new coordinate system?

Regards

[MrSharan]

Why am I here? I don't understand shit.