filmov
tv
Math Encounters - Primes and Zeros: A Million-Dollar Mystery

Показать описание
How can we quickly determine how many primes there are less than some huge number? The great mathematician Georg Friedrich Bernhard Riemann proposed a solution 160 years ago — but we still haven't been able to verify his hypothesis. Join mathematician Brian Conrey, founding Executive Director of the American Institute of Mathematics, as he shares some of the colorful history surrounding the world's greatest-ever math challenge.
Math Encounters is a public presentation series celebrating the spectacular world of mathematics, presented by the Simons Foundation and the National Museum of Mathematics.
For further information, call the National Museum of Mathematics at
Math Encounters is a public presentation series celebrating the spectacular world of mathematics, presented by the Simons Foundation and the National Museum of Mathematics.
For further information, call the National Museum of Mathematics at
Math Encounters - Primes and Zeros: A Million-Dollar Mystery
Math Encounters -- Patterns and Disorder
The hidden link between Prime Numbers and Euler's Number
An Exact Formula for the Primes: Willans' Formula
Math Encounters -- The Man Who Loved Only Numbers -- Paul Hoffman (Presentation)
Math Encounters -- On the Shoulders of Giants: Newton Revealed
Math Encounters -- Peeling the World
Math Encounters -- 'Star Trek: The Math of Khan' with James Grime
Math Encounters -- This Game is Rigged! How math can make you a winner”
Math Encounters - Blown Away: What Knot to Do When Sailing (Presentation)
Math Encounters — Online: “Number Theory Problems: From Easy to Undecidable”
Math Encounters: The Lonely Runner: an unsolved mystery of mathematics — M. Beck on April 13, 2022
The Riemann Hypothesis, Explained
Math Encounters - Blown Away: What Knot to Do When Sailing (Activity)
Math Encounters — Online: “Mathemagic with a Deck of Cards'
Math Encounters - 'The Wall of Fire Theorem: A Story of Mathematical Discovery'
Math Encounters - How Fast Does It Grow?
Math Encounters -- Andreas Daniel Matt - An Interactive Journey Through the Many Worlds of Geometry
Math Encounters -- The Man Who Loved Only Numbers -- Joel Spencer (Workshop)
Euler’s Pi Prime Product and Riemann’s Zeta Function
Math Encounters - 'Irrational Investigation: Why Pi Sometimes Equals 4'
Math Encounters - Paradoxes in Probability: Surprising Results and Why They Matter
Math Encounters -- Marc Chamberland - Single Digits: The Wonders of One to Nine
Math Encounters -- Soap Bubbles and Mathematics -- Frank Morgan (Presentation)
Комментарии
 1:18:02
1:18:02
 0:59:49
0:59:49
 0:12:29
0:12:29
 0:14:47
0:14:47
 0:45:14
0:45:14
 1:20:19
1:20:19
 1:22:06
1:22:06
 1:05:52
1:05:52
 1:17:34
1:17:34
 0:49:55
0:49:55
 0:49:07
0:49:07
 0:56:40
0:56:40
 0:16:24
0:16:24
 0:23:54
0:23:54
 1:21:14
1:21:14
 0:59:21
0:59:21
 0:57:46
0:57:46
 1:04:08
1:04:08
 0:44:54
0:44:54
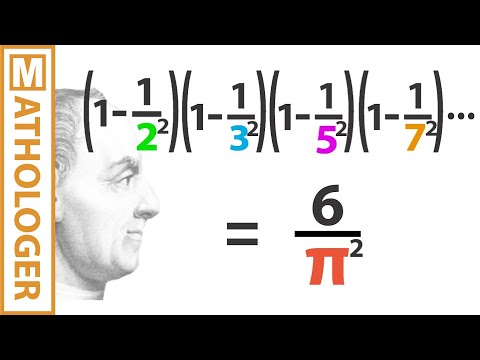 0:15:23
0:15:23
 1:04:38
1:04:38
 1:13:07
1:13:07
 1:14:58
1:14:58
 0:54:46
0:54:46