filmov
tv
12. The Einstein field equation.
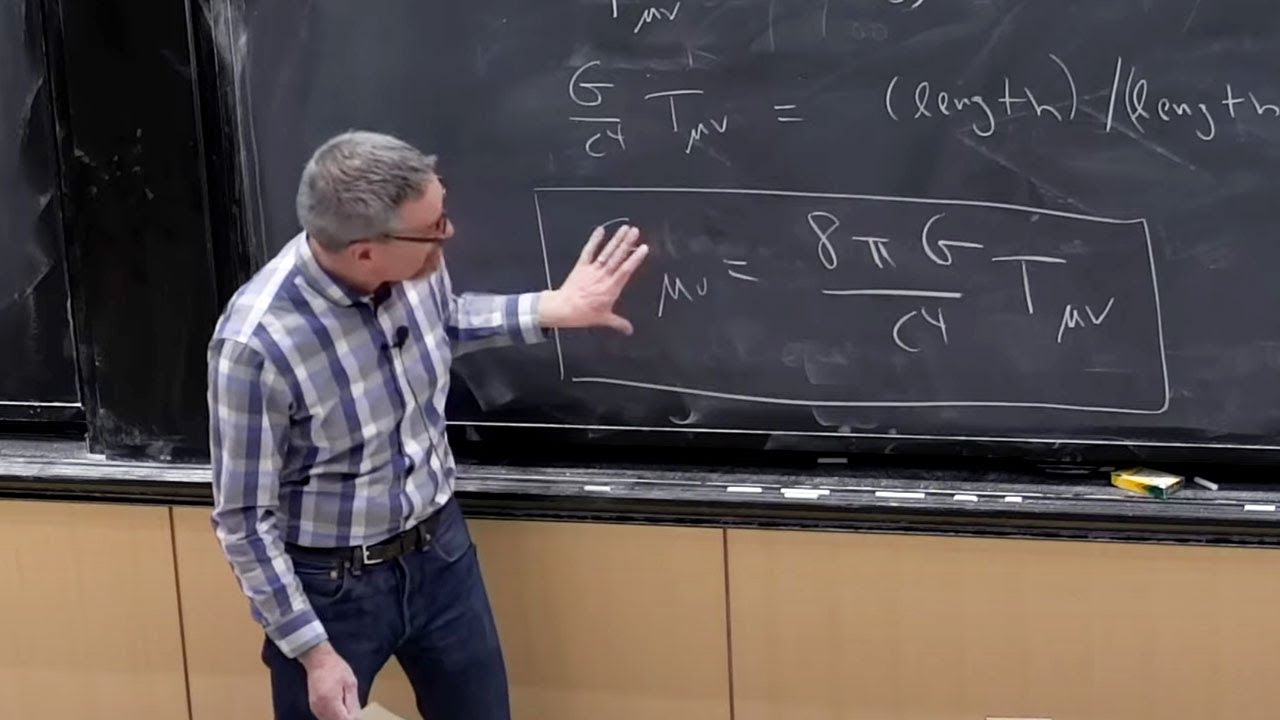
Показать описание
MIT 8.962 General Relativity, Spring 2020
Instructor: Scott Hughes
The Einstein curvature tensor, a variation on the Ricci curvature, defined so that it has vanishing covariant divergence. Using this tensor, we at last build a field theory for spacetime, motivating the Einstein field equation by arguing how to generalize a gravitational field equation to relativity.
License: Creative Commons BY-NC-SA
Instructor: Scott Hughes
The Einstein curvature tensor, a variation on the Ricci curvature, defined so that it has vanishing covariant divergence. Using this tensor, we at last build a field theory for spacetime, motivating the Einstein field equation by arguing how to generalize a gravitational field equation to relativity.
License: Creative Commons BY-NC-SA
12. The Einstein field equation.
General Relativity, Lecture 12: Einstein's field equations
How Mass WARPS SpaceTime: Einstein's Field Equations in Gen. Relativity | Physics for Beginners
Relativity 107f: General Relativity Basics - Einstein Field Equation Derivation (w/ sign convention)
Einstein's Field Equations of General Relativity Explained
13. The Einstein field equation (variant derivation).
The Maths of General Relativity (7/8) - The Einstein equation
Gravity Visualized
Chevarra Hansraj: Solving the Einstein Field Equations
Einstein field equation from action
Einstein Field Equation | Dr. Jacobus Verbaarschot | Suborno Isaac | Stony Brook University
The Einstein Field Equations | Tensor Calc Finale
Relativity 108a: Schwarzschild Metric - Derivation
What does Einstein field equations mean?
Schwarzchild solution(solution of Einstein field equation)
Einstein Field Equations Derivation | From The Einstein-Hilbert Action
Newtonian Limit (Lecture #12a of a course on Relativity & Cosmology)
Einstein Field Equation Uncovered
Einstein field equations | Einstein field equations explained | What is Einstein field equation
Derivation of Einstein Field Equations from Einstein-Hilbert Action
Last Words of Albert Einstein #shorts
10 General Relativity Linearized Gravity and Einstein's Field Equation
Einstein field equations | Einstein field equations explained | General theory of relativity
Einstein field equations | Einstein field equations explained | General theory of relativity
Комментарии
 1:17:40
1:17:40
 1:08:31
1:08:31
 0:14:15
0:14:15
 0:36:51
0:36:51
 0:28:23
0:28:23
 1:18:33
1:18:33
 0:07:29
0:07:29
 0:09:58
0:09:58
 0:01:23
0:01:23
 0:30:03
0:30:03
 0:27:44
0:27:44
 0:35:24
0:35:24
 0:30:48
0:30:48
 0:00:34
0:00:34
 0:37:01
0:37:01
 0:10:24
0:10:24
 0:15:30
0:15:30
 0:07:20
0:07:20
 0:01:41
0:01:41
 0:02:52
0:02:52
 0:00:37
0:00:37
 0:39:50
0:39:50
 0:32:50
0:32:50
 0:46:03
0:46:03